P-diviseurs
Olympiades mathématiques, énigmes et défis
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 19 Mai 2007, 20:00
par mt2sr » 19 Mai 2007, 20:00
définition:
soient m,p,d des entiers positives
p>0
on dit que d est un p-diviseur de m ssi
*

* d divise

et ne divise pas

donc
les monodiviseurs de m sont les diviseurs de m
questions : Montrer que le nombre des bi-diviseurs de
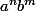
est
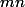
a et b sont des facteurs premiers
-
redwolf
- Membre Relatif
- Messages: 115
- Enregistré le: 08 Fév 2006, 11:00
-
 par redwolf » 19 Mai 2007, 20:47
par redwolf » 19 Mai 2007, 20:47
Bonsoir,

et

ne sont-ils pas supposés premiers entre eux quand même ?
-
mt2sr
- Membre Naturel
- Messages: 74
- Enregistré le: 07 Mai 2007, 11:48
-
 par mt2sr » 19 Mai 2007, 20:55
par mt2sr » 19 Mai 2007, 20:55
même plus ils sont deux nombres premiers distincts
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 22 Juil 2007, 18:46
par aviateurpilot » 22 Juil 2007, 18:46
\in[|1,n|]\times [|0,2m|]:\ a^{n+i}b^{j})
est un bi-diviseur de

don le nombre des bi-diviseurs de

est

au nombre des ces
_{\forall(i,j)\in[|1,n|]\times [|0,2m|]})
qui es egale à

.
donc tu as fait une faute ou bien j'ai fait une faute, :hein:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Aoû 2007, 21:59
par aviateurpilot » 14 Aoû 2007, 21:59
il est evident que les bi-diviseurs de
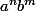
sont de la forme

ou bien

tel que

,
mtn on prend
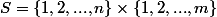
donc le nombre des bi-diviseurs de
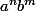
est:
\in S|\ a^{n+i}b^{m-j}<a^nb^m\}+card\{(i,j)\in S|\ a^{n-i}b^{m+j}<a^nb^m\})
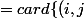\in S|\ a^{i}<b^j\}+card\{(i,j)\in S|\ b^{j}<a^i\})
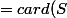)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités