Question sur les suites

[Imane69]

Bonsoir,

Il m'est demandé de prouver que Vn = 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)

On a dans les données : Vn = U(2n) - U(n) [2n et n comme indices]

et : Un = 1 + (1/2) + (1/3) + ... + (1/n)

Voilà, merci.

[capitaine nuggets]

Salut !

Bonsoir,

Il m'est demandé de prouver que Vn = 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)

On a dans les données : Vn = U(2n) - U(n) [2n et n comme indices]

et : Un = 1 + (1/2) + (1/3) + ... + (1/n)

Voilà, merci.

Je te demanderais bien ce que tu as fait, mais j'ai la flemme... :we:
Exprime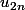 en fonction de puis remarque que les termes de sont contenus dans .
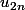Du coup, quand tu calculeras la différence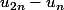 , il y a des choses qui disparaîtrons pour laisser place au résultat escompté !

:+++:

[Imane69]

Merci pour la réponse. Oui, j'ai réussi à avoir U(2n) = (1/2) U(n) mais après quand je U(2n)-Un je ne vois pas comment je pourrais arriver à la deuxième expression de V(n).

EDIT : Maintenant j'ai compris ce qu'il faut faire, merci. :D

[capitaine nuggets]

Merci pour la réponse. Oui, j'ai réussi à avoir U(2n) = (1/2) U(n) mais après quand je U(2n)-Un je ne vois pas comment je pourrais arriver à la deuxième expression de V(n).

EDIT : Maintenant j'ai compris ce qu'il faut faire, merci.

C'est faux ! :hum: (Tu peux le vérifier par le calcul).
Je te redemande donc de m'exprimer .

[Imane69]

U2n = 1 + (1/2) + (1/3) + (1/4) + ... + (1/n) + 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)
N'est-ce pas ? En fait au début je croyais que je ne devais avoir que des nombres pairs au dénominateur. Maintenant si on soustraie membre par membre on obtiendra U2n - Un = 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)

Juste après on nous demande de démontrer que ln[(2n+1)/(n+1)] J'ai démontré avant que Un > ln(1+n)

Là j'arrive à démontrer que ln[(2n+1)/(n+1)] < V(n) sans le "ou égale" en utilisant Un > ln(1+n) mais je ne sais pas si c'est la bonne façon et pour ce qui est de V(n)

[Imane69]

U2n = 1 + (1/2) + (1/3) + (1/4) + ... + (1/n) + 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)
N'est-ce pas ? En fait au début je croyais que je ne devais avoir que des nombres pairs au dénominateur. Maintenant si on soustraie membre par membre on obtiendra U2n - Un = 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)

Juste après on nous demande de démontrer que ln[(2n+1)/(n+1)] J'ai démontré avant que Un > ln(1+n)

Là j'arrive à démontrer que ln[(2n+1)/(n+1)] < V(n) sans le "ou égale" en utilisant Un > ln(1+n) mais je ne sais pas si c'est la bonne façon et pour ce qui est de V(n)

[capitaine nuggets]

U2n = 1 + (1/2) + (1/3) + (1/4) + ... + (1/n) + 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)
N'est-ce pas ? En fait au début je croyais que je ne devais avoir que des nombres pairs au dénominateur. Maintenant si on soustraie membre par membre on obtiendra U2n - Un = 1/(n+1) + 1/(n+2) + 1/(n+3) + ... + 1/(2n)

Juste après on nous demande de démontrer que ln[(2n+1)/(n+1)] ln(1+n)

Là j'arrive à démontrer que ln[(2n+1)/(n+1)] ln(1+n) mais je ne sais pas si c'est la bonne façon et pour ce qui est de V(n) <ou égale ln2 je ne vois pas trop comment m'y prendre ...

Ben, montre moi ce que tu as fait, je te dirais :lol3:

[Imane69]

D'accord, merci :
0 < ln(1+n) < U(n)
0 < ln(1+2n) < U(2n)

U(2n)-U(n)> ln(1+2n)-ln(1+n)
Vn > ln ((2n+1)/(1+n))

Voilà, pour la deuxième partie avec ln2, je ne sais pas quoi faire.

[capitaine nuggets]

D'accord, merci :
0 ln(1+2n)-ln(1+n)
Vn > ln ((2n+1)/(1+n))

Voilà, pour la deuxième partie avec ln2, je ne sais pas quoi faire.

Aïe aïe aïe, j'en étais sûr :we:
Bien qu’alléchant simple et direct, ce raisonnement est faux, voici pourquoi :

, toutefois, on peux s'en sortir en montrant que, pour tout réel , .

[Imane69]

Ah oui ... Ça rendait les choses étrangement faciles.

On a dans les données 1/(x+1) < ln(x + 1) - ln x < 1/x mais je ne sais pas si ça peut nous servir à quelque chose.

Je ne vois pas trop comment on va arriver à ln[(2n+1)/(n+1)]

[capitaine nuggets]

On a dans les données 1/(x+1) < ln(x + 1) - ln x < 1/x mais je ne sais pas si ça peut nous servir à quelque chose.

Mais si !!! :we:
C'est exactement ce qu'il nous faut !

.

Prenons, de façon générale, un terme de cette somme : , où .
A partir de la double inégalité, effectue (séparément), les actions suivantes :
1°) Minore
2°) Majore

[Imane69]

Si c'est à partir de la double inégalité, on peut avoir une majoration mais une minoration ? Elle sera minorée par 0 ?

Ou peut être :

1/ 1/(n+k) < ln((k+n/n))

2/ 1/(n+k) > - 1/n

[capitaine nuggets]

.

Prenons, de façon générale, un terme de cette somme : , où .
A partir de la double inégalité, effectue (séparément), les actions suivantes :
1°) Minore
2°) Majore

J'aurai dû être plus précis :lol3:

La double inégalité peut se voir comme deux inégalités :
et .
Pour montrer ce qu'on veut, on va minorer et majorer séparément (sans double inégalité).

Commençons par la majoration :

On a pris un terme quelconque de la somme de donc il faut minoré ce terme à l'aide de .

[Imane69]

Si on remplace x par n et 1 par k ça nous donnera 1/(n+k) < ln(n+k)-ln(n) mais je crois que pour minorer 1/(n+k) il faudra inverser le signe pour avoir - 1/(n+k) > ln(n) - ln(n+k), non ?

[capitaine nuggets]

Si on remplace x par n et 1 par k ça nous donnera 1/(n+k) ln(n) - ln(n+k), non ?

Attention, j'ai dit une bêtise : on majore ici :lol3:
non, il faut remplacer x+1 directement par n+k.

[Imane69]

Donc ce sera 1/(n+k) < ln(n+k)-ln(n) pour la majoration.
Pour la minoration on utilisera l'autre partie de l'inégalité pour avoir ln(n+k)-ln(n) < 1/n ?

[capitaine nuggets]

Je te montre le côté Vn < ln(2), il faudra faire de même avec l'autre côté.

Tu as 1/(x+1) < ln(x + 1) - ln x.
Or nous on veut 1/n+k donc il faut remplacer x+1 par n+k.
Toutefois, si on remplace x+1 par n+k, il faut remplacer x par n+k-1.
Ainsi, on a 1/(n+k) < ln(n+k) - ln(n+k-1).

Pour k=1, 1/(n+1) < ln(n+1) - ln(n) ;
Pour k=2, 1/(n+2) < ln(n+2) - ln(n+1) ;
Pour k=3, 1/(n+3) < ln(n+3) - ln(n+2) ;
...
Pour k=n, 1/(2n) < ln(2n) - ln(2n-1).

En faisant la somme membre à membre, on a :
1/(n+1)+1/(n+2)+1/(n+3)+...+1/(2n) < (ln(n+1) - ln(n)) + (ln(n+2) - ln(n+1)) + (ln(n+3) - ln(n+2)) +...+ (ln(2n) - ln(2n-1))

Sachant que dans le membre de droite, les termes en rouge se simplifient deux à deux, il reste alors :

Vn < ln(2n) - ln(n)

Je te laisse conclure :+++:

[Imane69]

Merci beaucoup, j'ai finalement réussi à comprendre ce qu'il fallait faire.