TS - Suites, Intégrales, Ln
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 10:49
par mella12 » 23 Avr 2013, 10:49
Bonjour, il y a une question que je n'arrive pas dans mon DM, quelqu'un peut m'aider svp, merci. Voici l'énoncé :Soit n un entier naturel non nul. On appelle dn, l'aire, en unités d'aires, du domaine du plan délimité par la courbe (C) d'équation
=ln(1+e^{-x})+\frac{1}{3}x)
, la droite (D) d'équation

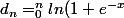dx)
On admet que pour tout réel x,
 \leq e^{-x})
Montrer que pour tout entier naturel n supérieur ou égal à 1,

. La suite
_{n} \geq 1)
est-elle convergente ?
-
nansyann
- Membre Naturel
- Messages: 67
- Enregistré le: 03 Nov 2012, 15:30
-
 par nansyann » 23 Avr 2013, 10:56
par nansyann » 23 Avr 2013, 10:56
mella12 a écrit:Bonjour, il y a une question que je n'arrive pas dans mon DM, quelqu'un peut m'aider svp, merci. Voici l'énoncé :Soit n un entier naturel non nul. On appelle dn, l'aire, en unités d'aires, du domaine du plan délimité par la courbe (C) d'équation
=ln(1+e^{-x})+\frac{1}{3}x)
, la droite (D) d'équation

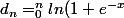dx)
On admet que pour tout réel x,
Montrer que pour tout entier naturel n supérieur ou égal à 1,

. La suite
_{n} \geq 1)
est-elle convergente ?
Faut s'aider de l'inégalité que l'on admet :
 \leq e^{-x})
Comme l'intégrale conserve l'ordre on a :
dx \leq \bigint_{0}^{n} e^{-x} dx)



-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 10:57
par ampholyte » 23 Avr 2013, 10:57
Bonjour,
Tu sais que
 \leq e^{-x})
Donc tu sais que :
 dx \leq \bigint_{0}^{n} e^{-x} dx)
0 partir de là que vaut :

???
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 11:16
par mella12 » 23 Avr 2013, 11:16
ampholyte a écrit:Bonjour,
Tu sais que
 \leq e^{-x})
Donc tu sais que :
 dx \leq \bigint_{0}^{n} e^{-x} dx)
0 partir de là que vaut :

???




-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 12:48
par ampholyte » 23 Avr 2013, 12:48
Peux-tu comparer 1 et

?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 14:07
par mella12 » 23 Avr 2013, 14:07
ampholyte a écrit:Peux-tu comparer 1 et

?


donc

car


-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 14:16
par ampholyte » 23 Avr 2013, 14:16
Hum la rédaction n'est pas super :

D'où :
[/TEX]\bigint_{0}^{n}e^{-x}dx \leq 1[/TEX]
Or
dx \leq \bigint_{0}^{n}e^{-x}dx \leq 1)
Donc

-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 14:28
par mella12 » 23 Avr 2013, 14:28
Oui d'accord et donc elle est convergente parce que elle est majorée par 1 c'est ça ?

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 14:32
par ampholyte » 23 Avr 2013, 14:32
Attention ce n'est pas parce quelle est majorée qu'elle converge.
Etudie la croissance de la suite.
PS : es-tu sûr de ce que tu as marqué
_n \geq 1)
dans ton premier post ?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 14:57
par mella12 » 23 Avr 2013, 14:57
ampholyte a écrit:Attention ce n'est pas parce quelle est majorée qu'elle converge.
Etudie la croissance de la suite.
PS : es-tu sûr de ce que tu as marqué
_n \geq 1)
dans ton premier post ?
Pour la croissance je fais Un+1 - Un ? Ca me gene avec l'integrale c'est pour ça que j'évitais de le faire..
C'est plutôt
_{n \geq 1})
mais je ne sais pas si ça change quelque chose, elle me parait bizarre cette écriture.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 15:06
par ampholyte » 23 Avr 2013, 15:06
D'accord, je comprends mieux.
Cette écriture signifie simplement la suite dn pour tout n supérieur ou égale à 1

Alors il faut en effet calculer U(n+1) - Un
Pourquoi est-ce que cela te gène ?
Tu sais que
 dx - \bigint_{0}^{n} g(x) dx = \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) dx - \bigint_{0}^{n} g(x) dx \\= \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) - g(x) dx)
d'après la relation de chasles.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 15:54
par mella12 » 23 Avr 2013, 15:54
ampholyte a écrit:D'accord, je comprends mieux.
Cette écriture signifie simplement la suite dn pour tout n supérieur ou égale à 1

Alors il faut en effet calculer U(n+1) - Un
Pourquoi est-ce que cela te gène ?
Tu sais que
 dx - \bigint_{0}^{n} g(x) dx = \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) dx - \bigint_{0}^{n} g(x) dx \\= \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) - g(x) dx)
d'après la relation de chasles.
Ah bon ! Je ne connaissais pas cette formule ! Mais ici il y a qu'une fonction : f(x) donc cela ferai
 dx - \bigint_{0}^{n} f(x) dx = \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) dx - \bigint_{0}^{n} f(x) dx \\= \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) - f(x) dx = \bigint_{n}^{n+1} f(x) dx ??)

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 16:02
par ampholyte » 23 Avr 2013, 16:02
Et oui tout à fait (j'ai ajouté g(x) pour généraliser) et que donne cette intégrale (surtout le signe qui est intéressant pour savoir si croissant ou non) ? =)
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 23 Avr 2013, 16:03
par jlb » 23 Avr 2013, 16:03
quel est le signe de f et qu'en déduis-tu en intégrant de n à n+1?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 16:34
par mella12 » 23 Avr 2013, 16:34
Ca doit être négatif mais je ne vois pas comment le justifier..
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 16:38
par mella12 » 23 Avr 2013, 16:38
Euh non positif si elle doit être croissante.. En fait je sais pas..

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 16:41
par ampholyte » 23 Avr 2013, 16:41
N'oublie pas qu'une intégrale représente l'aire sous la courbe. Or entre n et n + 1, quelle est le signe de ln(1 + e^(-x)) ? Donc l'intégrale sera (positive/négative)?
Donc la suite est (croissante / décroissante) ?
Si la suite est croissante et majorée alors elle converge.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 17:07
par mella12 » 23 Avr 2013, 17:07
C'est positif donc la suite est croissante et convergente vers 1

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 23 Avr 2013, 17:53
par ampholyte » 23 Avr 2013, 17:53
C'est ça
Tu aurais pu également repartir de

-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 23 Avr 2013, 18:10
par mella12 » 23 Avr 2013, 18:10
En fait j'ai fais comme on avait dans une correction d'un autre dm, c'est à dire
 \geq 0)
donc
dx \geq 0)
mais ça revient au meme que
dx \geq \bigint_{n}^{n+1} 0 dx)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 181 invités
, la droite (D) d'équation
. La suite
est-elle convergente ?
dans ton premier post ?
 dx - \bigint_{0}^{n} g(x) dx = \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) dx - \bigint_{0}^{n} g(x) dx \\= \bigint_{n}^{n+1} f(x) dx + \bigint_{0}^{n} f(x) - g(x) dx)