Bonjour, je voudrais savoir si quelqu'un pourrait m'aider à résoudre cet exercice ^^
Un fabricant de pièces de fonderie réalise une production mensuelle de q centaines de pièces d'un même modèle (0 ;) q ;) 10).
Le coût total de production, exprimé en milliers d'euros, est donné par*: C(q) = q³ 12q² + 60q
On assimile le coût marginal au rang q à la dérivée de coût total*: Cm(q) = C'(q). Le coût moyen, par centaine de pièces, est donnée par CM(q) = C(q)/q
1) Exprimer le coût marginal en fonction de q, pour q ;)[0;10].
2) Exprimer le coût, moyen en fonction de q ;) ]0;10].
3) Que peut-on dire du coût moyen lorsquil est égal au coût marginal*? Quelle est alors la valeur de la production*?
ES Dérivée
10 messages
- Page 1 sur 1
Tu pourrais d'abord nous expliciter davantage ce que tu ne comprends pas, parce que tu as les formules du Cm et CM données. Pour la question 1, c'est de la dérivation basique que tu as déjà dû voir en cours (pour les formules, voir mon nota). La 2 est une simple division et la 3 est une équation Cm = CM.
N.B :' = n.x^{n-1} \quad (k.x)' = k)
N.B :
D'accord mais j'ai essayée de mettre en place la formule qu'on a vue en cours pour la question 1 : c'est à dire :
Cm(q) = C(q+1) - C(q)
Cm(q) = q³ - 12q² + 60q
Cm(q) = (q+1)³ - 12 (q+1)² + 60 (q+1) - q³- 12q² + 60q
Cm(q) = 3q + (1 - 24 + 60) = 3q +37
Cm(q) = C'(q) = 3q+37
Je voudrais savoir si c'est bien ça...
Cm(q) = C(q+1) - C(q)
Cm(q) = q³ - 12q² + 60q
Cm(q) = (q+1)³ - 12 (q+1)² + 60 (q+1) - q³- 12q² + 60q
Cm(q) = 3q + (1 - 24 + 60) = 3q +37
Cm(q) = C'(q) = 3q+37
Je voudrais savoir si c'est bien ça...
Je te conseille vivement de lui préférer cette formule-ci, beaucoup plus directe :
 = C'(q))
Je t'ai donné les deux seules formules dont tu as besoin plus-haut mais tes formules de dérivation basiques, indispensables, sont à connaître !
La formule que tu as choisi d'utiliser, quoique plus intuitive, est à exclure car plus longue, à moins qu'on te demande de directement calculer le coût marginal de production de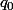 unités.
unités.
Ta réponse est d'ailleurs erronée, pour plusieurs raisons. Dès la deuxième ligne, ta formulation est incorrecte, à la troisième tu oublies de changer le signe, et pour passer à la quatrième il aurait fallu utiliser les formules de ces identités remarquables :
^3 = a^3 + b^3 + 3a^2b + 3ab^2} \quad et \quad {(a + b)^2 = a^2 + b^2 + 2ab})
 = C(q+1) - C(q))
 = [(q+1)^3 -12(q+1)^2 + 60(q+1)] - [q^3 - 12q^2 + 60q])
 = [(q^3 + 1^3 + 3q^2 + 3q) - 12(q^2 + 1^2 + 2q) + 60q + 60] - q^3 + 12q^2 - 60q)
 = (q^3 - q^3) + (3q^2 - 12q^2 + 12q^2) + (3q - 24q + 60q - 60q) + (1 - 12 + 60))
 = 3q^2 - 21q + 47)
Ton exercice t'exhorte à utiliser la formule de la dérivée, beaucoup plus rapide (1 ligne au lieu de 5 !). Essaye, et dis-moi ton résultat.
Je t'ai donné les deux seules formules dont tu as besoin plus-haut mais tes formules de dérivation basiques, indispensables, sont à connaître !
La formule que tu as choisi d'utiliser, quoique plus intuitive, est à exclure car plus longue, à moins qu'on te demande de directement calculer le coût marginal de production de
Ta réponse est d'ailleurs erronée, pour plusieurs raisons. Dès la deuxième ligne, ta formulation est incorrecte, à la troisième tu oublies de changer le signe, et pour passer à la quatrième il aurait fallu utiliser les formules de ces identités remarquables :
Ton exercice t'exhorte à utiliser la formule de la dérivée, beaucoup plus rapide (1 ligne au lieu de 5 !). Essaye, et dis-moi ton résultat.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
