Dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 17:59
par Alexandrat22 » 11 Nov 2012, 17:59
Bonjour. J'ai une fonction f à dérivée, mais je n'y arrive pas.
Soit f la fonction définie sur [0 ; +00[ par :

Je vois que c'est de la forme
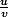
avec u=

et u'=

v=

et v'=
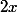
On à donc f'(x) =
-xe^{-x}(2x)}{(x^2+1)^2})
Ensuite je suis bloquée pour développer.
Est-ce que c'est f'(x)=
^2})
?
Merci de m'aider.
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 18:04
par sylvainp » 11 Nov 2012, 18:04
Salut,
u est aussi de la forme u*v avec u=x et v=exp(-x), tu as donc (uv)'=u'v+v'u
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 18:10
par Alexandrat22 » 11 Nov 2012, 18:10
Ok je vais donc essayer de refaire la dérivée avec cet élément. Merci
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 18:26
par Alexandrat22 » 11 Nov 2012, 18:26
J'obtiens donc

=
}{x^2+1})
=

Ensuite est-ce que je met cette fraction sous la forme
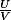
?
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 18:43
par sylvainp » 11 Nov 2012, 18:43
Attention, comme tu l'avais dit dans ton premier message, ta fonction est de la forme u/v ! ton raisonnement pour calculer la dérivée d'un quotient était donc correct : (u/v)'= (u'v-v'u)/v².
Par contre, c'est un peu compliqué car u au numérateur est un produit de fonction u=U*V, donc la dérivée u' se calcule u'=U'V+V'U , c'est ce que je veux indiquer dans mon premier message.
U=x
V=exp(-x)
u=U*V=x*exp(-x)
v=x²+1
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 19:04
par Alexandrat22 » 11 Nov 2012, 19:04
sylvainp a écrit:Attention, comme tu l'avais dit dans ton premier message, ta fonction est de la forme u/v ! ton raisonnement pour calculer la dérivée d'un quotient était donc correct : (u/v)'= (u'v-v'u)/v².
Par contre, c'est un peu compliqué car u au numérateur est un produit de fonction u=U*V, donc la dérivée u' se calcule u'=U'V+V'U , c'est ce que je veux indiquer dans mon premier message.
U=x
V=exp(-x)
u=U*V=x*exp(-x)
v=x²+1
On à donc si j'ai bien compris : u=

et u'=

=

v=

et v'=
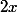
J'obtiens donc f'(x) =
-xe^-^x(2x)}{(x^2+1)^2})
f'(x) =
^2)
C'est bien ça ? car je ne suis pas sur de ma dernière dérivation de f.
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 19:09
par sylvainp » 11 Nov 2012, 19:09
Il reste une petite erreur dans le calcul de u'=U'V+V'U
U'=1
V=exp(-x)
U=x
V'=-exp(-x)
donc u'=exp(-x)-x*exp(-x)
et non pas u'=x comme tu trouves
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 19:16
par Alexandrat22 » 11 Nov 2012, 19:16
sylvainp a écrit:Il reste une petite erreur dans le calcul de u'=U'V+V'U
U'=1
V=exp(-x)
U=x
V'=-exp(-x)
donc u'=exp(-x)-x*exp(-x)
et non pas u'=x comme tu trouves
Ah oui j'ai fais une erreur.
Du coup on à : f'(x)=
(x^2+1))-((x*e^-^x)2x)}{(x^2+1)^2)
?
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 19:21
par sylvainp » 11 Nov 2012, 19:21
Ouais parfait!
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 19:22
par Alexandrat22 » 11 Nov 2012, 19:22
sylvainp a écrit:Ouais parfait!
Par contre je ne sais pas trop comment m'y prendre pour développer
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 19:41
par sylvainp » 11 Nov 2012, 19:41
tu peux factoriser par exp(-x) au numérateur, ça fait exp(-x)(1-x-x²-x^3) au numérateur si je me suis pas trompé
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 19:43
par Alexandrat22 » 11 Nov 2012, 19:43
Alexandrat22 a écrit:Par contre je ne sais pas trop comment m'y prendre pour développer
Est-ce qu'en développent en obtient :
f'(x) =
^2})
?
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 19:44
par Alexandrat22 » 11 Nov 2012, 19:44
Je vais essayer de factoriser alors
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 20:03
par Alexandrat22 » 11 Nov 2012, 20:03
Alexandrat22 a écrit:Est-ce qu'en développent en obtient :
f'(x) =
^2})
?
Lorsque je factorise par
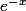
avec le développement que j'ai fais au dessus, j'obtiens pour le numérateur :
)
J'ai du faire une erreur mais je ne voie pas où.
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 20:16
par sylvainp » 11 Nov 2012, 20:16
l'erreur est dans le calcul de -(x(exp(-x))*2x ça fait pas -3x*exp(-x) mais -2x²*exp(-x) tu retrouves le résultats que j'ai écrit un peu avant
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 20:21
par Alexandrat22 » 11 Nov 2012, 20:21
sylvainp a écrit:l'erreur est dans le calcul de -(x(exp(-x))*2x ça fait pas -3x*exp(-x) mais -2x²*exp(-x) tu retrouves le résultats que j'ai écrit un peu avant
Ah oui d'accord. Et une fois factorisée, on obtient
}{(x^2+1)^2})
mais le calcul n'est pas fini là ? Je ne voie pas se qu'il faut faire pour poursuivre le calcul.
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 11 Nov 2012, 20:34
par sylvainp » 11 Nov 2012, 20:34
Non tu ne peux pas aller plus loin, et le résultat est plutôt lisible comme ça.
-
Alexandrat22
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Nov 2012, 17:29
-
 par Alexandrat22 » 11 Nov 2012, 20:42
par Alexandrat22 » 11 Nov 2012, 20:42
sylvainp a écrit:Non tu ne peux pas aller plus loin, et le résultat est plutôt lisible comme ça.
D'accord, merci beaucoup de votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 149 invités