Bonjour, j'ai un peu de difficulté à définir le lien entre la continuité et la dérivabilité. Et aussi, je ne sais pas comment expliquer l'utilité des formules de dérivations, en fait je sais qu'une dérivée d'une fonction donne la pente d'une tangente en un point. Cependant, quelle est l'utilité des formules de dérivations.
Puisque je dois être capable de dire ce qu'est une dérivée et ce qu'est l'utilité des formules de dérivation, ce qui semble être deux choses différentes.
Merci beaucoup, bonne journée
Continuité et dérivabilité et autres
11 messages
- Page 1 sur 1
MyriSweeney a écrit:Bonjour, j'ai un peu de difficulté à définir le lien entre la continuité et la dérivabilité. Et aussi, je ne sais pas comment expliquer l'utilité des formules de dérivations, en fait je sais qu'une dérivée d'une fonction donne la pente d'une tangente en un point. Cependant, quelle est l'utilité des formules de dérivations.
Puisque je dois être capable de dire ce qu'est une dérivée et ce qu'est l'utilité des formules de dérivation, ce qui semble être deux choses différentes.
Merci beaucoup, bonne journée
Bonjour,
continu veut dire sans cassure une fonction lisse qui pour passer de x à x+h avec h petit on doit faire un saut petit.
derivable veut dire que la derive est non infini et que cette dérivé est la meme pour x->a- que x->a+.
Par exemple x->valeur absolue de x est continue non dérivable
dérivable -> continue
MyriSweeney a écrit:Pouvez-vous me donner un exemple d'un dérivée qui est dérivable et une autre qui ne l'est pas?
Salut,
Tu parles de classes de régularité là : une fonction est dite de classe C1 si sa dérivée est continue sur I.
Elle est dite de classe C0 si elle est continue sur I, de classe C2 si sa dérivée seconde est continue sur I et Cn si elle est n fois continûment dérivable sur I.
Elle est de classe Cinfini si on peut la dériver indéfiniment (la plupart des fonctions que tu abordes durant le secondaire sont de cette classe-là).
Pour te donner un exemple de fonction dont la dérivée est indérivable sur R, peut y avoir par exemple une primitive de arccos(cos x) (attends je t'en donnerai peut-être une formule tout à l'heure si j'arrive à transformer l'expression).
Ce sont pas des exemples très faciles à trouver.
Pour répondre à ta question du début, la notion de dérivée est primordiale dans toutes les sciences dures : maths, physique, chimie, bio, micro-économie, ...
En cinématique et en mécanique, tu verras que le mouvement d'un point peut être analysé par son accélération et sa vitesse qui sont respectivement la dérivée seconde et la dérivée de sa position par rapport au temps.
En thermodynamique, la plupart des systèmes sont modélisés par une variation d'entropie.
En chimie, la cinétique d'une réaction est déterminée à partir d'une loi de vitesse basée sur l'évolution de la dérivée temporelle de la concentration d'un réactif. On utilise aussi le calcul intégral pour voir la question d'un sens inverse.
En biologie, les scientifiques posent des équations aux dérivées partielles (EDP) pour effectuer des modèles complexes : évolution de la population d'une espèce donnée dans un milieu donné et soumise à des contraintes (nourriture, lutte pour sa survie, ...).
La liste n'est bien entendu pas exhaustive.
L'analyse mathématique (calcul différentiel et calcul intégral) est au coeur de l'avancée scientifique. Elle permet une analyse poussée de systèmes de plus en plus complexes.
En cinématique et en mécanique, tu verras que le mouvement d'un point peut être analysé par son accélération et sa vitesse qui sont respectivement la dérivée seconde et la dérivée de sa position par rapport au temps.
En thermodynamique, la plupart des systèmes sont modélisés par une variation d'entropie.
En chimie, la cinétique d'une réaction est déterminée à partir d'une loi de vitesse basée sur l'évolution de la dérivée temporelle de la concentration d'un réactif. On utilise aussi le calcul intégral pour voir la question d'un sens inverse.
En biologie, les scientifiques posent des équations aux dérivées partielles (EDP) pour effectuer des modèles complexes : évolution de la population d'une espèce donnée dans un milieu donné et soumise à des contraintes (nourriture, lutte pour sa survie, ...).
La liste n'est bien entendu pas exhaustive.
L'analyse mathématique (calcul différentiel et calcul intégral) est au coeur de l'avancée scientifique. Elle permet une analyse poussée de systèmes de plus en plus complexes.
MyriSweeney a écrit:Bonjour, j'ai un peu de difficulté à définir le lien entre la continuité et la dérivabilité. Et aussi, je ne sais pas comment expliquer l'utilité des formules de dérivations, en fait je sais qu'une dérivée d'une fonction donne la pente d'une tangente en un point. Cependant, quelle est l'utilité des formules de dérivations.
Puisque je dois être capable de dire ce qu'est une dérivée et ce qu'est l'utilité des formules de dérivation, ce qui semble être deux choses différentes.
Merci beaucoup, bonne journée
on peut trouver des fonctions particulières, comme:
f(x)=x² si x est irrationnel
f(x)=0 si x rationnel
f est continue uniquement en 0
f est également dérivable en 0
@MyriSweeney
Quelques explications supplémentaires
1)
Lorsqu'une fonction f est dérivable , on calcule la fonction dérivée sur le domaine de définition avec l'aide des formules données dans ton cours de maths
avec l'aide des formules données dans ton cours de maths
Le signe de cette fonction dérivée, (donc il faut faire une étude de signe de l'expression) en fonction de
en fonction de  ) , va te permettre de tracer un tableau de variations de la fonction
) , va te permettre de tracer un tableau de variations de la fonction  , puis de tracer très précisément une représentation graphique de cette fonction
, puis de tracer très précisément une représentation graphique de cette fonction  (en faisant également un tableau de valeurs)
(en faisant également un tableau de valeurs)
2)
La 2ième notion importante à retenir est : le nombre) est la pente de la tangente au point d'abscisse
est la pente de la tangente au point d'abscisse  de
de 
et DONC si=0) alors
alors  admet en ce point une tangente horizontale
admet en ce point une tangente horizontale
Par exemple : dans un tableau de variation , tu pourras constater que tous les points dits "extremum local" ( maximum ou minimum) on a :=0) , et donc tu peux en conclure qu'en tous ces points la tangente à la courbe
, et donc tu peux en conclure qu'en tous ces points la tangente à la courbe  est horizontale
est horizontale
3)
Dernier commentaire : Comme
si f est dérivable en a alors f est continue en a
on a donc
si f n'est pas continue en a alors f n'est pas dérivable en a
Quelques explications supplémentaires
1)
Lorsqu'une fonction f est dérivable , on calcule la fonction dérivée sur le domaine de définition
Le signe de cette fonction dérivée, (donc il faut faire une étude de signe de l'expression
2)
La 2ième notion importante à retenir est : le nombre
et DONC si
Par exemple : dans un tableau de variation , tu pourras constater que tous les points dits "extremum local" ( maximum ou minimum) on a :
3)
Dernier commentaire : Comme
si f est dérivable en a alors f est continue en a
on a donc
si f n'est pas continue en a alors f n'est pas dérivable en a
@MyriSweeney
Exemples de fonction continue en un point non dérivable en ce point
) =|
=|  | en
| en  (fonction valeur absolue)
(fonction valeur absolue)
 =\sqrt{x}) en
en  (attention
(attention  )
)
) = |
= | ) | en
| en  et en
et en  , en
, en  ...etc....
...etc....
Exemples de fonction non continue
=\frac{1}{x}) n'est pas continue sur
n'est pas continue sur 
c'est la fonction inverse qui n'est pas définie en x=0 donc attention
Cette fonction est continue sur et est continue sur
et est continue sur 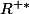
=E(x)) (fonction partie entière) est continue par morceau sur
(fonction partie entière) est continue par morceau sur 
Cette fonction n'est pas continue en tout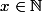
Exemples de fonction continue en un point non dérivable en ce point
Exemples de fonction non continue
c'est la fonction inverse qui n'est pas définie en x=0 donc attention
Cette fonction est continue sur
Cette fonction n'est pas continue en tout
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 168 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
