Exercice limites, dérivabilité, continuité, ....

par **Zebulon** » 25 Nov 2006, 21:49

Baba a écrit:Et ben ca fait pas f'(0)=lim g(x) quand x tend vers 0.

Si ! On demandait de montrer que g est continue en 0, c'est-à-dire que

ou encore

.
Or on sait que

, donc... ?

par **shtefi** » 25 Nov 2006, 22:08

Salut !

On pose :
g(-x) = [rac(1+(-x)²) - 1] / (-x) = -[rac(1+x²) - 1] / x = - g(x)

Donc g est impaire.
Si g avait été paire, on aurait eu, g(-x) = g(x)

par **Baba** » 25 Nov 2006, 22:13

shtefi t'es un petit peu en retard mais merci quand même !

En première page j'ai dit que j'avais trouvé ca, et puis ca m'a été confirmé.

Dsl Zebulon mais là je comprends vraiment pas.... :triste: :triste: :triste: :triste: :cry: :cry: :cry: :cry:

par **Zebulon** » 25 Nov 2006, 22:35

Pas de panique ! On veux montrer que :
[quote="Zebulon"]

existe, alors

car g est impaire. Je te laisse essayer de le justifier. On peut donc parler de

, toujours si elle existe.

Maintenant l'autre égalité :
on sait que

. Mais que vaut f'(0) ?
Montre-moi comment tu rédigerais.

par **Baba** » 25 Nov 2006, 22:51

Je sais pas du tout comment rédiger........ :briques:

f'(0) ne serait pas égal à 0/2 ou 0/(-2) soit 0 ????

par **Zebulon** » 26 Nov 2006, 09:08

C'est

, mais ça fait toujours 0 !
On a alors montré que

.
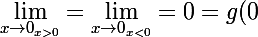C'est exactement dire que g est continue en 0.

par **Baba** » 26 Nov 2006, 15:12

OK merci en reprenant tout depuis le début ca va j'ai compris.

Maintenant il faut que je determine

Bon la sur ces limites et continuités j'en chie à mort......

par **Zebulon** » 26 Nov 2006, 15:15

Baba a écrit:OK merci en reprenant tout depuis le début ca va j'ai compris.

Maintenant il faut que je determine

Bon la sur ces limites et continuités j'en chie à mort......

C'est exactement pareil ! Pose

. La limite que tu cherches est la dérivée de h en 0.

par **Baba** » 26 Nov 2006, 15:17

OK.

Ouais je me doutais qu'il y allait avoir une analogie mais j'en étais pas sur !

par **Baba** » 26 Nov 2006, 15:28

Moi je trouve

Parce que

et

Non ?

par **Zebulon** » 26 Nov 2006, 15:35

Baba a écrit:Moi je trouve

Parce que et

C'est parfait ! :++:
Pour le premier "=", précise quand même dans ta copie "par définition de la dérivée de h en 0", ça ne fait pas de mal et ça montre au prof que tu as compris.

par **Baba** » 26 Nov 2006, 15:51

Maintenant, je dois prouver que la fonction g est dérivable en 0.

Il faut que je fasse quoi ?

J'ai une très vague idée et je suis pas convaincu que ce soit bon.

par **Zebulon** » 26 Nov 2006, 16:02

Baba a écrit:J'ai une très vague idée et je suis pas convaincu que ce soit bon.

Quelle est cette vague idée ? :happy3:

par **Baba** » 26 Nov 2006, 16:06

Je sais pas trop peut etre qu'il faut que je prouve

Mais je suis pas convaincu du tout, et surtout je vois pas comment faire

par **julian** » 26 Nov 2006, 16:10

Cette formule est bonne avec le (très) léger détail que c'est la définition de la dérivé g'(x), et non f'(x) :++:

par **Zebulon** » 26 Nov 2006, 16:11

julian a écrit:Cette formule est bonne avec le (très) léger détail que c'est la définition de la dérivé g'(x), et non f'(x) :++:

... et que c'est en 0 : =g'(0).

par **Zebulon** » 26 Nov 2006, 16:14

Baba a écrit:Je sais pas trop peut etre qu'il faut que je prouve

Mais je suis pas convaincu du tout, et surtout je vois pas comment faire

Comme le dit Julian, c'est la définition. Donc rien à prouver. Ce qu'il faut prouver, c'est que cette limite existe en x=0. En fait, tu l'as même déjà calculée...

par **Baba** » 26 Nov 2006, 16:19

Bon si tu dis que je l'ai deja calculée c'est que ca doit être le cas.

Faut que je retrouve ca ....

par **Zebulon** » 26 Nov 2006, 16:25

Quand x=0, combien vaut

?

par **julian** » 26 Nov 2006, 16:28

g'(x)!!!!!!!! :ptdr: :ptdr: :ptdr:
Okay j'effacerai....

Exercice limites, dérivabilité, continuité, ....

Qui est en ligne