Exercice limites, dérivabilité, continuité, ....
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 23 Nov 2006, 21:49
par Baba » 23 Nov 2006, 21:49
Salut a tous !!
Voilà, je vous expose mon problème.
J'ai une fonction définie sur R par:
g= [racine de(1+x²) - 1] / x pour x différent de 0 et g(0)=0
Et dès la première question, ben je sais plus comment faire.
--->>> 1°) Etudier la parité de g.
(Je me souviens plus du tout comment faut faire, mais il me semble que c'est tout bête)
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
 par bitonio » 23 Nov 2006, 21:55
par bitonio » 23 Nov 2006, 21:55
tu calcules f(-x) alias remplacer x par -x
a-t-on f(-x)=f(x) ou f(-x)=-f(x) ?
Bonne chance
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 23 Nov 2006, 22:09
par Baba » 23 Nov 2006, 22:09
Perso, je trouve g(-x)= -g(x)
Mais je suis pas convaincu de ce que j'ai fait.
Une confirmation ?
Ce que j'ai trouvé voudrait dire qu'elle est impaire. Non ?
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 00:41
par Baba » 25 Nov 2006, 00:41
Personne pour confirmer ?
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 25 Nov 2006, 01:08
par rene38 » 25 Nov 2006, 01:08
Bonsoir
Confirmation : pour



-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 10:55
par Baba » 25 Nov 2006, 10:55
OK merci beaucoup !!
Ca veut donc bien dire que cette fonction est impaire !
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 11:04
par Baba » 25 Nov 2006, 11:04
Après il faut que je prouve que la fonction g est continue en 0, et évidemment j'arrive a une forme indéterminée 0/0.
Il faut donc que je lève l'indetermination, mais j'avoue ne pas avoir de réelle idée là !
:mur:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 11:09
par Zebulon » 25 Nov 2006, 11:09
Bonjour,
si j'écris que pour
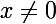
,
={\sqrt{1+x^2}-\sqrt{1+0^2}\over x-0})
, ça te donne des idées ?
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 11:18
par Baba » 25 Nov 2006, 11:18
Je dois avouer que la ca m'inspire pas plus....
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 11:26
par Zebulon » 25 Nov 2006, 11:26
OK. Soit la fonction f définie sur
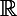
par
=\sqrt{1+x^2})
.
Quelle est la valeur (par le calcul habituel) de la dérivée de f en 0 ?
D'autre part, quelle est, par définition de la dérivée d'une fonction en un point, l'expression de sa dérivée en 0 ?
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 11:56
par Baba » 25 Nov 2006, 11:56
=1/(2\sqrt{2x})=(f(x+h)-f(x))/h)
C'est pas ca ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 12:13
par Zebulon » 25 Nov 2006, 12:13
Baba a écrit:=1/(2\sqrt{2x}))
Non, recalcule-la.
Presque...
=\lim\limits_{h\to 0} {f(x+h)-f(x)\over h})
. Donc f'(0)=...? (exprime-la en fonction de g)
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 12:21
par Baba » 25 Nov 2006, 12:21
=2x/(2\sqrt{1+x^2}))
Ca doit plutôt être ça.
Par contre exprimer
)
en fonction de
)
j'y arrive pas trop....
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 16:18
par Baba » 25 Nov 2006, 16:18
Bon a cette question ou il faut que je prouve la continuité de g en 0, ben j'y arrive toujours pas !
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 17:25
par Zebulon » 25 Nov 2006, 17:25
Baba a écrit:=2x/(2\sqrt{1+x^2}))
Ca doit plutôt être ça.
Oui, c'est plutôt ça ! :we: Remarque que ça peut se simplifier.
Par contre exprimer
)
en fonction de
)
j'y arrive pas trop....
Par définition de la dérivée de f en 0,
=\lim\limits_{x\to0}{f(x)-f(0)\over x-0})
, on est d'accord ?
Remplace f(x) et f(0) dans cette fraction. Ca donne ?
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 20:13
par Baba » 25 Nov 2006, 20:13
Il faut que je remplace f(x) et f(0) dans cette fraction par quoi ?
g(x) et g(o) ?
Dsl mais j'ai du mal a visualiser ce que l'on est en train de faire là.
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 21:00
par Zebulon » 25 Nov 2006, 21:00
Baba a écrit:Il faut que je remplace f(x) et f(0) dans cette fraction par quoi ?
Par leurs valeurs !
=\sqrt{1+x^2})
.
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 21:15
par Baba » 25 Nov 2006, 21:15
Ah ok !!! lol
=\lim\limits_{x\to0}{\sqrt(1+x^2)-\sqrt(1)\over x-0})
Donc ca fait ca.
Mais j'ai toujours du mal a voir ou je vais arriver.......
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Nov 2006, 21:24
par Zebulon » 25 Nov 2006, 21:24
Baba a écrit:=\lim\limits_{x\to0}{\sqrt(1+x^2)-\sqrt(1)\over x-0})
C'est ça.
Mais j'ai toujours du mal a voir ou je vais arriver.......
Pourtant on y est !!! Essaie d'exprimer f'(0) en fonction de g(x). Il ne faut pas chercher midi à 14 heures !
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 25 Nov 2006, 21:32
par Baba » 25 Nov 2006, 21:32
Et ben ca fait pas f'(0)=lim g(x) quand x tend vers 0.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités



