Bonjour. Soit K un corps, E un K-ev, f endomorphisme de E. On note H un supplementaire de Ker(f) dans E et G un supplementaire de Im(f) dans E.
1)montrer que g:H-->Im(f) x--> f(x) est un isomorphisme lineaire.
j'ai montré que g est bien défini et linéaire, je bloque sur la bijectivité(injectif plus surjectif).Il faut aussi montrer que pour x ds E, il existe un unique(y,z) de G*H tq x= y+f(z)(le faire par analyse synthèse?).
2)On note g l'application de E ds E qui a x associe cet unique z(de l'écriture precedente).déterminer le noyau et l'image de g(je n'ai pas d'idéees, surtout pour Im(g).
Merci
Exo espaces vectoriels
6 messages
- Page 1 sur 1
Salut
c'est 'surjectif' et non pas 'subjectif'
H au lieu de h (1ere ligne)
====
pour montrer que g est injectif il suffit que tu montres que si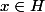 et
et =0) alors
alors  et ça tu peux le faire si tu traduit
et ça tu peux le faire si tu traduit =0) à l'appartenance au noyau d'une application linéaire (autre que g) .... et tu utilise une prpriété des sous-espaces supplémentaires ....
à l'appartenance au noyau d'une application linéaire (autre que g) .... et tu utilise une prpriété des sous-espaces supplémentaires ....
Pour montrer que g est surjective tu prend y \in Im f donc il existe tq
tq =y) Tu décompose x suivant H et ... et tu verras
Tu décompose x suivant H et ... et tu verras
benjilbos a écrit:Bonjour. Soit K un corps, E un K-ev, f endomorphisme de E. On note H un supplementaire de Ker(f) dans E et G un supplementaire de Im(f) dans E.
1)montrer que g:H-->Im(f) x--> f(x) est un isomorphisme lineaire.
j'ai montré que g est bien défini et linéaire, je bloque sur la bijectivité(injectif plus subjectif).Il faut aussi montrer que pour x ds E, il existe un unique(y,z) de G*H tq x= y+f(z)(le faire par analyse synthèse?).
2)On note h l'application de E ds E qui a x associe cet unique z(de l'écriture precedente).déterminer le noyau et l'image de h(je n'ai pas d'idéees, surtout pour Im(h).
Merci
c'est 'surjectif' et non pas 'subjectif'
H au lieu de h (1ere ligne)
====
pour montrer que g est injectif il suffit que tu montres que si
Pour montrer que g est surjective tu prend y \in Im f donc il existe
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
