Théorème
22 messages
- Page 1 sur 2 - 1, 2
Théorème
Démontrer (de préférence une démonstration élémentaire) le théorème suivant:
soit p un nombra premier ; Si p s'écrit 4k+1 ou k est un entier naturel Alors il existent a et b entiers naturels tels que p=a²+b² , avec a et b uniques.
Enjoy!
soit p un nombra premier ; Si p s'écrit 4k+1 ou k est un entier naturel Alors il existent a et b entiers naturels tels que p=a²+b² , avec a et b uniques.
Enjoy!
J'essaye de réfléchir, mais je connais pas trop le programme du Lycée.
Sans le "langage des congruences", ça risque d'être assez lourd.
Aprés, je pense pas qu'il voient au Lycée le fait que, pour p premier et a non divisible par p on a
a^(p-1)=1 [mod p] et je sais pas quelle est la façon la plus rapide de le faire niveau Lycée.
Pour moi un truc rapide, c'est de passer par le Binôme de Newton, mais est-ce que c'est vu au Lycée ?
Sans le "langage des congruences", ça risque d'être assez lourd.
Aprés, je pense pas qu'il voient au Lycée le fait que, pour p premier et a non divisible par p on a
a^(p-1)=1 [mod p] et je sais pas quelle est la façon la plus rapide de le faire niveau Lycée.
Pour moi un truc rapide, c'est de passer par le Binôme de Newton, mais est-ce que c'est vu au Lycée ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, alors j'essaye.... (tout suggestion/amélioration est... bienvenue ....)
Tout d'abord, la partie super façile (mais pas demandée) : Pour tout entier a, a² et soit multiple de 4 (si a pair) soit de la forme 4k+1 (si a est impair) donc a²+b² ne peut pas être de la forme 4k+3 : un nombre premiers de la forme 4k+3 ne peut pas s'écrire a²+b².
Dans l'autre sens, je propose une solution sous forme d'exo (T.S.+ Spé math : congruences)
Dans tout l'exercice désigne un nombre premier impair.
désigne un nombre premier impair.
1) Montrer que, pour tout entiers et
et 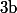 on a
on a ^p\equiv a^p+b^p\ [p])
Indication : Utiliser le binôme de Newton.
2) En déduire que, pour tout entier ,
,  puis que, si
puis que, si  n'est pas divisible par
n'est pas divisible par  , que
, que 
Indication : Récurence.
Dans toute la suite, on dira qu'un entier est un carré modulo
est un carré modulo 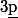 lorsqu'il existe un entier
lorsqu'il existe un entier  tel que
tel que  .
.
3) Montrer que, si est un carré modulo
est un carré modulo  alors
alors 
4) Montrer qu'il y a exactement entier
entier  qui sont des carrés modulo
qui sont des carrés modulo  puis qu'il y a au plus
puis qu'il y a au plus  entier
entier  qui sont solutions de
qui sont solutions de  . Que peut on en déduire ?
. Que peut on en déduire ?
5) En déduire que est un carré modulo
est un carré modulo  si et seulement si
si et seulement si  avec
avec 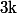 entier
entier
Dans toute la suite, on suppose que et on considère un entier
et on considère un entier  tel que
tel que  .
.
6) Montrer qu'il y a au moins couples d'entiers
couples d'entiers \not=(0,0)) tels que
tels que  puis en déduire qu'il existe au moins un couple d'entiers
puis en déduire qu'il existe au moins un couple d'entiers \not=(0,0)) tel que
tel que  et que
et que  divise
divise 
Indication : combien y a t'il de reste possibles pour la division de par
par  ?
?
7) Montrer que, pour un tel couple) , on a forcément
, on a forcément  puis qu'il existe au moins une solution à l'équation
puis qu'il existe au moins une solution à l'équation  avec
avec  .
.
Tout d'abord, la partie super façile (mais pas demandée) : Pour tout entier a, a² et soit multiple de 4 (si a pair) soit de la forme 4k+1 (si a est impair) donc a²+b² ne peut pas être de la forme 4k+3 : un nombre premiers de la forme 4k+3 ne peut pas s'écrire a²+b².
Dans l'autre sens, je propose une solution sous forme d'exo (T.S.+ Spé math : congruences)
Dans tout l'exercice
1) Montrer que, pour tout entiers
Indication : Utiliser le binôme de Newton.
2) En déduire que, pour tout entier
Indication : Récurence.
Dans toute la suite, on dira qu'un entier
3) Montrer que, si
4) Montrer qu'il y a exactement
5) En déduire que
Dans toute la suite, on suppose que
6) Montrer qu'il y a au moins
Indication : combien y a t'il de reste possibles pour la division de
7) Montrer que, pour un tel couple
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:J'essaye de réfléchir, mais je connais pas trop le programme du Lycée.
Sans le "langage des congruences", ça risque d'être assez lourd.
Aprés, je pense pas qu'il voient au Lycée le fait que, pour p premier et a non divisible par p on a
a^(p-1)=1 [mod p] et je sais pas quelle est la façon la plus rapide de le faire niveau Lycée.
Pour moi un truc rapide, c'est de passer par le Binôme de Newton, mais est-ce que c'est vu au Lycée ?
Salut,
Oui on voit le petit théorème de Fermat en T°S (mais pas sa généralisation, le théorème d'Euler, par contre) ainsi que le binôme de Newton.
Moi la démo que j'aime bien c'est celle utilisant un raisonnement combinatoire avec un collier de perles mais après les goûts et les couleurs ...
Disons qu'en fait le "fils conducteur" de la preuve est trés nettement "comment déterminer les carrés modulo p". Seule les deux questions finales vont vraiment dans le sens de la question de départ : le reste est beaucoup plus général.benekire2 a écrit:Moi celle que je connais est celle de Ben ( D'ailleurs les question sur le théorème de Fermat est du cours mais ça fait pas de mal ) , je la trouve très naturelle mais pas très intuitable quand même !!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Effectivement :je modifie...Matt_01 a écrit:D'ailleurs on sent que le final est déjà plus exotique.
A part ça, il y a une petite coquille, il faut lire.
Tient, je viens de réagir aussi qu'il manque des questions concernant l'unicité de (a,b).
Je sais pas si on s'en sort façilement dans cette "veine" (i.e. sans les entiers de Gauss).
Donc "DEFI" : rajouter quelques questions pour montrer l'unicité...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Je propose pour cela :
On suppose que avec
avec 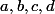 entiers naturels.
entiers naturels.
-Montrer que(ad+bc)) est divisible par
est divisible par  .
.
-En déduire que divise l'un des deux facteurs.
divise l'un des deux facteurs.
On suppose que divise
divise 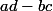 .
.
-Comparer^2+(ac+bd)^2) et
et (c^2+d^2))
-En déduire que est divisible par
est divisible par  .
.
-Montrer alors qu'il existe tel que
tel que 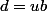 et
et 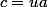 (on pourra utiliser la comparaison précédente)
(on pourra utiliser la comparaison précédente)
-Conclure.
Puis on admet que la démonstration lorsque divise
divise 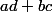 est similaire.
est similaire.
On suppose que
-Montrer que
-En déduire que
On suppose que
-Comparer
-En déduire que
-Montrer alors qu'il existe
-Conclure.
Puis on admet que la démonstration lorsque
Matt_01 a écrit:Par contre, je trouve le point juste avant la conclusion un peu plus vache que les autres.
Cette question fera office de mini challenge :we:
Perso, c'est plutôt le premier point qui m'a un peu posé problème : est-ce qu'on s'en sort simplement sans écrire que
Pour le dernier point, on a la somme des carrés de deux nombres divisibles par p (dont un clairement non nul) qui fait p² et ça ne laisse pas bien le choix... (mais vu ton "il existe u tel que...", je me demande si tu ne procède pas différement)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Matt_01 a écrit:Pour le premier point on dévelloppe :
Pour le dernier point, on est amené àet donc
et
sont colinéaires.
Pour le premier point : OK (c'est moi qui suis un manche)
Mais, pour le dernier point, vu que
De plus, ad=bc (tout seul) implique a=c et b=d vu que a,b sont premiers entre eux et c,d aussi (évident vu que a²+b²=p=c²+d²)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
