Arithmétique :D

[S.L]

Trouver tous les couples d'entiers (a,b) tels que: (ab) divise (a²+b²).
Bonne chance!

[Ben314]

Salut,
(forme cannonique) donc est entier et
Vu que et sont de même parité, les 2 solutions pour sont (2,2) et (-2,-2).
Dans le premier cas et donc
Dans le deuxième cas et donc

[S.L]

Très bien ^^

[Matt_01]

Hello,
Quitte à diviser par le carré de , on peut supposer a et b premiers entre eux.
On suppose . On écrit 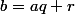la division euclidienne de par .
Alors Cette quantité est donc entière ssi l'est.
Or ces deux rationnels sont inférieurs à : leur somme vaut alors .
En multipliant par ab on obtient : En passant l'égalité modulo b on obtient divisible par et donc 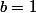(car a et b premiers entre eux) puis .
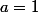De manière générale, au final .

[S.L]

Merci, jolie^^

[Ben314]

Sans vouloir te vexer Matt_01, partant de , je suis pas sûr qu'il faille autant de lignes pour en déduire que :
On a donc or donc

[Matt_01]

C'est pas faux :marteau:
J'ai juste pensé que c'était plus compliqué que ça l'était donc j'ai sorti "l'artillerie" sans regarder en arrière ...

[jack01]

Salut,
(forme cannonique) donc est entier et
Vu que et sont de même parité, les 2 solutions pour sont (2,2) et (-2,-2).
Dans le premier cas et donc
Dans le deuxième cas et donc

c'est tres jolie master Ben314;bonne solution