Arithmétique : nombres premiers et divisibilité
38 messages
- Page 1 sur 2 - 1, 2
Arithmétique : nombres premiers et divisibilité
Bonsoir,
j'ouvre un post que j'utiliserai pour poster tous les exos sympas sur ce theme.
On commence par un exercice tres facile :
"Soit p un nombre premier. Montrer qu'il existe un diviseur premier de p^p - 1 et est congru à 1 modulo p."
j'ouvre un post que j'utiliserai pour poster tous les exos sympas sur ce theme.
On commence par un exercice tres facile :
"Soit p un nombre premier. Montrer qu'il existe un diviseur premier de p^p - 1 et est congru à 1 modulo p."
salut
pour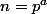 (puissance d'un nombre premier)
(puissance d'un nombre premier)
(*) soient un premier divisant
un premier divisant 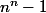 tel que
tel que 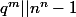 et
et 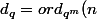)
on a)=pgrc(n,q-1)) .
.
soit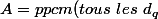) qui divisera
qui divisera  bien sure et donc
bien sure et donc 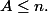
on a donc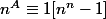 donc
donc 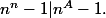
ce qui donne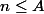 . d'ou
. d'ou 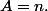
puisque les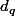 ne sont qui des puissances de
ne sont qui des puissances de  alors
alors 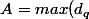=n) donc
donc 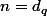 pour un certain
pour un certain 
finalement ce premier verifiant
verifiant 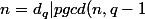|q-1) donc
donc 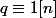
je vais voire le cas de quelconque apres ((je me prepare pour le concours lol))
quelconque apres ((je me prepare pour le concours lol))
pour
(*) soient
on a
soit
on a donc
ce qui donne
puisque les
finalement ce premier
je vais voire le cas de
Quelqun veut il poster la solution à cet exo ?
Personnellement voici la mienne :
soit k le plus petit entier tel que p^k = 1 [mod q], q désignant un diviseur premier de p^p - 1
k est l'odre de p modulo q
pour tout entier a tel que p^a = 1 [mod q], a est un multiple de k
ici on a
p^p = 1 [q]
fermat => p^(q-1) = 1 [q]
donc
d = PGCD(p , q-1) = k
k divise p
donc k = 1 ou p
si k = p pour un certain q c'est fini car p divisera q - 1 donc q = 1 [p]
si k = 1 pour tout q premier divisant p^p - 1, alors
p^k = p = 1 [q]
donc q divise p-1
or
p^p-1 = (p-1)*(p^(p-1) + p^(p-2) + ... + p + 1)
comme p-1 ne divise pas (p^(p-1) + p^(p-2) + ... + p + 1)
on a l'existence d'au moins un x entier premier divisant (p^(p-1) + p^(p-2) + ... + p + 1) et non p-1
en particulier x divise p^p - 1
et x ne divise pas p-1
contradiction
Personnellement voici la mienne :
soit k le plus petit entier tel que p^k = 1 [mod q], q désignant un diviseur premier de p^p - 1
k est l'odre de p modulo q
pour tout entier a tel que p^a = 1 [mod q], a est un multiple de k
ici on a
p^p = 1 [q]
fermat => p^(q-1) = 1 [q]
donc
d = PGCD(p , q-1) = k
k divise p
donc k = 1 ou p
si k = p pour un certain q c'est fini car p divisera q - 1 donc q = 1 [p]
si k = 1 pour tout q premier divisant p^p - 1, alors
p^k = p = 1 [q]
donc q divise p-1
or
p^p-1 = (p-1)*(p^(p-1) + p^(p-2) + ... + p + 1)
comme p-1 ne divise pas (p^(p-1) + p^(p-2) + ... + p + 1)
on a l'existence d'au moins un x entier premier divisant (p^(p-1) + p^(p-2) + ... + p + 1) et non p-1
en particulier x divise p^p - 1
et x ne divise pas p-1
contradiction
lapras a écrit:Ok pour la démo aviateurpilot, toujours tres condensé ton LaTex :we:
Bravo !
je voulais montrer le resultat vrai pour tous n au debut,mais quand j'ai trouvé que A=ppcm(des d_q).
alors j'ai pris le cas particulier ou n est une puissance d'un nombre premier pour que ppcm(des d_q)=max des d_p. lol.
je vais chercher pour l'autre cas apres. a+
Pas trop dur celui la... :++:
On fixe p,q premier >1000 avec p>a, et on note p(0)=p et p(n+1)=ap(n)+bq.Tous les p(n) devraient etre censés etre premiers or par reccurence directe on a p(n)=[1+a+...+a^(n-1)]*b*q modulo p =(a^n-1)/(a-1)*b*q modulo p. Comme a^(p-1)=1 modulo p,pour n=p-1 on obtiens un terme divisible par p absurde
On fixe p,q premier >1000 avec p>a, et on note p(0)=p et p(n+1)=ap(n)+bq.Tous les p(n) devraient etre censés etre premiers or par reccurence directe on a p(n)=[1+a+...+a^(n-1)]*b*q modulo p =(a^n-1)/(a-1)*b*q modulo p. Comme a^(p-1)=1 modulo p,pour n=p-1 on obtiens un terme divisible par p absurde
38 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
