Equa Diff y''=C/y²

par **Mikel83** » 22 Oct 2010, 12:45

Bonjour!
Pour résoudre l'équation différentielle y''=C/y², j'ai multiplié les deux membres par y':
y'y'' = Cy'/y² ce qui me donne y'²/2 = -C/y + K ou y'² = -2C/y + 2K.
Ensuite, je bloque... Merci pour vos conseils

par **JeanJ** » 22 Oct 2010, 13:45

dy/dx = (+ou-)racine carrée(...)
Puis équa. dif. à variables séparées.

par **Mikel83** » 22 Oct 2010, 13:48

JeanJ a écrit:dy/dx = (+ou-)racine carrée(...)
Puis équa. dif. à variables séparées.

Merci pour ta réponse! Mais si je fais cette opération, je vais avoir 1/y dans le radical, et je ne vois pas comment faire la séparation des variables ?

par **arnaud32** » 22 Oct 2010, 14:10

tu vas devoir resoudre qqch du type:

par **Mikel83** » 22 Oct 2010, 14:26

arnaud32 a écrit:tu vas devoir resoudre qqch du type:

Ah, oui! Merci... Mais je ne sais pas comment ça s'intègre....

par **JeanJ** » 22 Oct 2010, 15:30

dt = y dy/racine( ? )
puis u = y²
du = ?

par **Mikel83** » 22 Oct 2010, 15:39

JeanJ a écrit:dt = y dy/racine( ? )
puis u = y²
du = ?

Bonjour JeanJ!
dt=dy/racine[2(K-C/y); pourquoi tu multiplies par y ?

par **arnaud32** » 22 Oct 2010, 16:30

tu peux commence par u=1/y peut etre

par **Mikel83** » 22 Oct 2010, 16:47

arnaud32 a écrit:tu peux commence par u=1/y peut etre

Bon, je me lance!

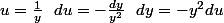
ce y² me gêne ...

par **arnaud32** » 22 Oct 2010, 16:50

tu dois avoir dt= f(u)du (les y doivent disparaitre)

par **Mikel83** » 22 Oct 2010, 16:53

arnaud32 a écrit:tu dois avoir dt= f(u)du (les y doivent disparaitre)

Dois je comprendre que u=1/y n'est pas le bon changement de variable?

Equa Diff y''=C/y²

Equa Diff y''=C/y²

Qui est en ligne