Solution maximale équa.diff : ppté de Cauchy mis en cause?

par **max** » 25 Mar 2007, 12:43

Bonjour!

J'ai l'ED suivante : xy' - 2y = x²

a) Résoudre ED0
b)En déduire la solution sur chacun des intervalles -oo 0; 0 +oo
c)Recherche des solutions sur R par analyse/synthese

J'ai résolu ces questions sans soucis particulier (après un prolongement en continuité en 0 et l'étude de dérivabilité en 0 il vient qu'il y a une infinité de solutions de l'équation différentielle sur R quelles que soient les valeurs de lambda1 et lambda2, les constantes provenant de la résolution de l'ED sur chacun des intervalles)

Cependant, on peut constater que chaque fonction solution sur R vérifient la solution initiale f(1)=1

L'existence et l'unicité d'une fonction solution vérifiant une condition initiale (Ppté de Cauchy) est elle alors érronée ?

Merci

par **allomomo** » 25 Mar 2007, 13:17

Salut,

]0, +\infty[
1 - (E0) :

Les solutions sont les fonctions de la forme :

est solution particulière (E). A toi de finir

par **max** » 25 Mar 2007, 13:23

allomomo a écrit:Salut,

]0, +\infty[
1 - (E0) :

Les solutions sont les fonctions de la forme :

est solution particulière (E). A toi de finir

oui oui merci j'ai trouvé tout cela

je n'arrive juste pas à conclure car le probleme de cauchy affirme qu'il n'y a QU'UNE fonction qui passe par f(1)=1 par exemple; aors qu'ici il y en a une infinité

Que conclure? Le probleme de Cauchy est dans l'erreur?

par **allomomo** » 25 Mar 2007, 13:37

Bon

d'ou

par **max** » 25 Mar 2007, 13:56

allomomo a écrit:Bon

d'ou

Merci mais je ne suis psa sur que tu comprenns ma question.

Mon prof a tracé plusieurs fonctions solutions de l'équation différentielle, passant toute par f(1)=1.

Il demande donc si cela remet en cause le Pb de Cauchy (UNICITE d'une solution vérifiant f(a)=b)

par **mathelot** » 25 Mar 2007, 14:25

bonjour,

le problème de Cauchy est posé pour une équation résoluble en y'
donc de la forme :

où

est une fonction de

dans

localement lipschitzienne.
Ton équation se scinde en deux problèmes de Cauchy sur deux intervalles disjoints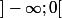

et

Parfois, on peut raccorder deux solutions pour obtenir une solution maximale,
mais il n'y a plus unicité.

par **max** » 25 Mar 2007, 14:34

mathelot a écrit:bonjour,

le problème de Cauchy est posé pour une équation résoluble en y'
donc de la forme :
où est une fonction de dans localement lipschitzienne.
Ton équation se scinde en deux problèmes de Cauchy sur deux intervalles disjoints et
Parfois, on peut raccorder deux solutions pour obtenir une solution maximale,
mais il n'y a plus unicité.

merci, mais comment le rédiger clairement?

par **mathelot** » 25 Mar 2007, 15:41

Analyse:

La forme des solutions de l'équation (E) sont les suivantes:
celles définies sur R+* et ne s'annulant pas sont de la forme:

celles définies sur R-* et n e s'annulant pas sont de la forme:

Elles correspondent à des solutions du problème de Cauchy maximales sur des parties connexes où l'équation est résoluble en y'.

L'équation n'interdit pas de chercher une ou des solutions définies sur R tout entier.

Pour obtenir une solution sur R tout entier, on doit faire un raccord
dérivable entre deux solutions, l'une définie sur R-*, l'autre sur R+*.

Synthèse:

Soit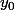

une solution sur R-* à un problème de Cauchy.
avec

(condition initiale).

Cette solution admet deux prolongements de classe

(continuement dérivable) en x=0.

- par la fonction nulle sur R+*
- par une solution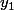

en ajustant les constantes

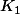et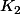

.

Conclusion: il ya donc existence d'une solution maximale sur R tout entier
à un problème de Cauchy mais pas unicité (Il y a toujours deux solutions au problème de Cauchy). ça vient du fait que l'équation n'est pas résoluble en y'
sur

tout entier.

par **max** » 25 Mar 2007, 16:00

mathelot a écrit:Analyse:

La forme des solutions de l'équation (E) sont les suivantes:
celles définies sur R+* et ne s'annulant pas sont de la forme:

celles définies sur R-* et n e s'annulant pas sont de la forme:

Elles correspondent à des solutions du problème de Cauchy maximales sur des parties connexes où l'équation est résoluble en y'.

L'équation n'interdit pas de chercher une ou des solutions définies sur R tout entier.

Pour obtenir une solution sur R tout entier, on doit faire un raccord
dérivable entre deux solutions, l'une définie sur R-*, l'autre sur R+*.

Synthèse:

Soit une solution sur R-* à un problème de Cauchy.
avec (condition initiale).

Cette solution admet deux prolongements de classe (continuement dérivable) en x=0.

- par la fonction nulle sur R+*
- par une solution en ajustant les constantes et .

Conclusion: il ya donc existence d'une solution maximale sur R tout entier
à un problème de Cauchy mais pas unicité (Il y a toujours deux solutions au problème de Cauchy). ça vient du fait que l'équation n'est pas résoluble en y'
sur tout entier.

j'ai compri!! merci beaucoup :id:

je vais encore potasser tout ça mais je crois que j'ai compri

par **mathelot** » 25 Mar 2007, 16:07

Plus imagé, quand une courbe solution "arrive" à l'origine,
la fonction dérivée a le choix en x=0 de la direction pour repartir.

par **Zebulon** » 25 Mar 2007, 17:47

mathelot a écrit:bonjour,

le problème de Cauchy est posé pour une équation résoluble en y'
donc de la forme :
où est une fonction de dans localement lipschitzienne.

Bonjour,
dans les hypothèses du problème de Cauchy, F doit être localement lipschitzienne uniquement par rapport à la deuxième variable.

Solution maximale équa.diff : ppté de Cauchy mis en cause?

Solution maximale équa.diff : ppté de Cauchy mis en cause?

Qui est en ligne