Anneaux spéciaux

[MJD]

Bonjour
Existe-t-il une dénomination particulière pour les anneaux finis commutatifs
dans lesquels tout élément non nul est soit une unité, soit un diviseur de zéro.
Si oui, y-a-t-il des études ou des publications sur ce sujet.
Merci

MJD

[Finrod]

Tout élément non inversible est nilpotent.

Comme l'anneau est fini, la famille des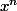 l'est aussi. Donc il existe n tel que ,

Autre remarque, si f est une unité (l'anneau ou on inverse f) et si f est un diviseur de 0, .

Donc tes anneaux ont un espace topologique de Zariski Trivial, avec seulement deux ouverts, le vide (associé à ) et l'espace total (associé à A)

En fait, ça les caractérise. Mais je ne connais pas de nom pour cette famille d'anneaux.
Et il y a sûrement beaucoup plus à en dire.

[Doraki]

Si A est un anneau fini commutatif et si x est dans A
ou bien le morphisme de groupes y:A -> x*y:A est bijectif, et x est inversible,
ou bien il l'est pas, et x est donc diviseur de 0.

Donc tu n'as qu'à les appeler des anneaux finis commutatifs.