Polynome minimal
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 13 Déc 2009, 21:15
par prody-G » 13 Déc 2009, 21:15
bonsoir à tous !!
je ne sais pas par où commencer avec cet exercice...
Soit E un K-ev de dimension finie et u dans L(E).
On note pour x dans E,

le polynôme de degré minimal et unitaire de l'idéal {
(x)=0)
}.
Montrer qu'il existe x dans E tel que
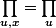
où ce dernier désigne le polynôme minimal de u.
Y avait une première question qui proposait de se placer dans le cas où

est de la forme

où P est irréductible et unitaire, et r un entier.
J'ai réussi ce cas là mais je ne vois pas comment faire dans le cas général.
Une idée ?

merci d'avance.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Déc 2009, 21:23
par Ben314 » 13 Déc 2009, 21:23
Bonsoir,
Il suffit de montrer que, pour tout x,y dans E, il existe un z tel que
=\prod_{u,z})
(pourquoi ?)
Ensuite, j'essayerais bien avec z=x+ty, où t est dans K bien choisi...(là je suis pas totalement sûr de moi)
Il y a peut être une autre méthode plus astucieuse, mais je pense que celle là marche...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
 par alavacommejetepousse » 13 Déc 2009, 22:08
par alavacommejetepousse » 13 Déc 2009, 22:08
bonsoir glabalement ce que dit ben avec t = 1
(ei) une base de E
1 le polynôme minimal noté Q de u est le ppcm des polynômes minimaux des ei
2 on décompose Q en produits de facteurs P^r
3 par définition du ppcm pour chaque P^r il existe un ei dont le polynôme minimal est un multiple de P^r
4 On trouve facilement un x dont le polynôme minimal est P^r
5 le point clé : on montre grâce à bezout que pour x et y de polynômes minimaux premiers entre eux le polynôme minimal de x+y est le produit des deux polynômes minimaux
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 19 Déc 2009, 18:18
par prody-G » 19 Déc 2009, 18:18
salut !
merci de vos réponses !
on m'a conseillé d'utiliser les sous espaces caractéristiques ce qui évite de décomposer Q en irréductibles et donne directement les P_r, apres on utilise ce que vous dites pour conclure, ie que x+y possède comme polynome minimal


thanks !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2009, 18:36
par Ben314 » 19 Déc 2009, 18:36
prody-G a écrit:salut !
merci de vos réponses !
on m'a conseillé d'utiliser les sous espaces caractéristiques ce qui évite de décomposer Q en irréductibles et donne directement les P_r, apres on utilise ce que vous dites pour conclure, ie que x+y possède comme polynome minimal


thanks !
Si ton corps de base est algébriquement clos, tu peut raisonner en terme de sous espace caractéristique car leur somme est l'espace tout entier. S'il n'est pas algébriquement clos, il faut soit le plonger dans sa cloture algébrique, soit faire ce que dit alavacommejetepousse (dans le cas non algébriquement clos, la décomposition du poly_char. en irréductible correspond à ce que l'on peut faire de plus proche de la décomposition en sous espaces caractéristique dans le cas algébriquement clos)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
prody-G
- Membre Relatif
- Messages: 376
- Enregistré le: 28 Mar 2006, 14:36
-
 par prody-G » 19 Déc 2009, 19:00
par prody-G » 19 Déc 2009, 19:00
ah oui merci

j'ai été maladroit, je parlais des Ker
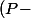(u))
)
comme je n'avais pas que Q=ppcm(minimaux des ei) on décomposait d'abord E par lemme des noyaux.
Merci encore !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Déc 2009, 19:02
par Ben314 » 19 Déc 2009, 19:02
Fait simplement attention que, si le corps n'est pas algébriquement clos, ton endomorphisme peut ne pas avoir de valeurs propres du tout !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
