Arithmétique !!!

[fourize]

bonjour,

je me suis attaqué à un exercice d'arithmétique aujourd'hui mais visiblement j'ai besoin d'un coup de pouce . voici l'énoncé :

soit a, b et c des entiers relatifs. et m >=0.
1_ on suppose que a divise b. montrer que divise ?
2_ soit p un nombre premier divisant ; montrer que p divise a. est ce toujours vrai si p n'est pas premier ?
3_ démontrer que si a et b divisent c et que pgdc(a,b)=1; alors ab divise c. est ce que c'est encore vrai si pgdc(a,b) différent de 1?

je dois avoué que, bien que j'ai bien lu mon cours, les idées m'échappe
pour la 1. j'ai fait:

a|b b = ka avec k relatif.
=
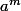
en posant k' = on a:
= k' (je conclus)

mais mon prof de TD n'a pas l'air d'accord. sans qu'il puisse me dire la faute.
j'aimerai savoir ou est l'erreur? et quelques tuyaux pour le 2 et 3 .

merci d'avance :triste:

[Lemniscate]

mon prof de TD n'a pas l'air d'accord

Ah bon ? c'est bizzare... Je pense pour ma part que ton raisonnement est tout à fait correct !

sans qu'il puisse me dire la faute

Heureusement ! Parce que y'en a pas ! (bon si je me plante j'aurais l'air bête mais j'en suis quasiment sûr)

Pour la 2 je te suggère d'utiliser la décomposition d'un nombre en puissances de facteurs premiers.

Pour la 3 aussi en fait.

Pour les "est-ce encore vrai" cherche d'abord des contre-exemples évidents

[fourize]

merci pour ta suggestion mais je m'y perds.

Pour la 2 je te suggère d'utiliser la décomposition d'un nombre en puissances de facteurs premiers.

moi même j'avais pensé faire:

comme p divise
= p*q
m^ = m^ *m^
au finale, on s'en sort pas puisque

au finale, on s'en sort pas. tu me comprends??
ainsi, sauf si je me trompe, c'est pas vraiment la bonne idée.

[Nightmare]

Bonsoir,

Ou sinon, on y va avec Gauss :

Si p ne divise pas a, p est premier avec a. Vu que on en déduit que p divise 1. Absurde.

[Lemniscate]

Ben en fait je pensais à décompser a en facteurs premiers. Si p ne figure pas dans la décomposition de a alors il ne figurera pas non plus dans celle de a^m ce qui conduit à une absurdité.

Pour la 3 tu sais que ab figure dans la décomposition en facteurs premiers de c car pgcd(a,b)=1 (pas de facteurs premiers en commun)

Cela dit peut-être est-ce un peu compliqué de recourir à cet outil pour résoudre cet exercice...

[leon1789]

mais mon prof de TD n'a pas l'air d'accord. sans qu'il puisse me dire la faute.
j'aimerai savoir ou est l'erreur? et quelques tuyaux pour le 2 et 3 .

Normal, tu utilises inutilement et à tord le symbole !
b = ka b^m = k^m a^m est faux ! Seule une implication est vraie... Celle qui est utile à l'exo.

Moralité : il faut peut-être arrêter d'utiliser le symbole , mais être plus minutieux avec un => ... :id:

[leon1789]

mais mon prof de TD n'a pas l'air d'accord. sans qu'il puisse me dire la faute.
j'aimerai savoir ou est l'erreur? et quelques tuyaux pour le 2 et 3 .

Je ne vois qu'une piste : b = ka b^m = k^m a^m est faux quand m est pair ... (en valeur absolue, c'est ok)

[leon1789]

Pour la 3), il suffit d'une ligne avec une relation de Bézout

[Lemniscate]

Effectivement c'est l'équivalence qui n'est pas exacte...
Mais ici on a besoin que du sens "direct" de l'implication.

[leon1789]

Mais ici on a besoin que du sens "direct" de l'implication.

oui ! donc autant perdre l'habitude d'écrire :id: un simple => est tout aussi efficace la plupart du temps , et plus sûr ! :id:

[yos]

autant perdre l'habitude d'écrire :id: un simple => est tout aussi efficace la plupart du temps , et plus sûr !

Surtout qu'un revient à questionner l'hypothèse, ce qui est un comble.

[Doraki]

Avoir un <=> c'est bien quand on se demande si on a le droit d'oublier l'hypothèse pour toujours et de quand même finir l'exo

[moimickey2]

Bonsoir à tous,

pour la question 1) ce qui gêne ton professeur (je me permets de te tutoyer...) c'est que ton affirmation cache une récurence. Tu peux montrer le résultat pa une récurrence sans faire appel à un arsenal d'outils trop puissants pour une telle question. De même pour la 2) si p divise a^m alors p divise a^(m-1) puisqu'il ne divise pas a et récurrence à rédiger.
Pour la 3) pense à écrire c=ka... je te laisse deviner la suite.

Bonne soirée et bon courage
Moimickey2

[yos]

pour la question 1) ce qui gêne ton professeur (je me permets de te tutoyer...) c'est que ton affirmation cache une récurence.

Ou ça une récurrence? Bien cachée?
a|b donc b=ka donc donc .
Dans l'égalité ?
Je ne partage pas ton opinion.

[moimickey2]

Bonjour,
c'était une idée sur ce qui aurait pu ne pas plaire au prof...
mais effectivement cela semble inutile...

Moimickey2

[fourize]

bonjour,
tout d'abord merci pour l'intérêt que vous porter à cet exercice,

Bonsoir à tous,

pour la question 1) ce qui gêne ton professeur (je me permets de te tutoyer...) c'est que ton affirmation cache une récurence. Tu peux montrer le résultat pa une récurrence sans faire appel à un arsenal d'outils trop puissants pour une telle question.

je ne vois pas trop ou se cache la recurence? en plus même si c'est le cas,
que ce qui géne?

De même pour la 2) si p divise a^m alors p divise a^(m-1) puisqu'il ne divise pas a et récurrence à rédiger.

la decomposition de a en facteurs premiers, anoncer par les autres (que j'en remerci d'ailleurs de leurs participations), me semble un peu bizarre, pour montrer que p divise a. il ne faut pas oublier qu'on part de l'hypothèse que p divise .
je suis d'accord avec toi sur la citation precedente, mais est il possible de rediger une reccurence (inverse)?? c'est de dire de partir de m, supposer m-1, et demontrer m=1 ?? :doh: je toujours eu à faire l'initiale, herediter; et conclusion ?? :triste:

Pour la 3) pense à écrire c=ka... je te laisse deviner la suite.
Moimickey2

la troisime, j'ai reussi à le faire hier soir; mais puisque tu me propose la meme procedure que ce que j'ai fait, tu merite ça :++:

cordialement,

[Lemniscate]

la decomposition de a en facteurs premiers, annoncée par les autres (que j'en remerci d'ailleurs de leurs participations), me semble un peu bizarre, pour montrer que p divise a. il ne faut pas oublier qu'on part de l'hypothèse que p divise a^m.

Tu pars de p divise a^m.

Tu supposes que p ne divise pas a (raisonnement par l'absurde).
Tu aboutis, en regardant juste cette supposition, à l'absurdité suivante : p ne divise pas a^m (ce que j'ai démontré dans un des messages précédents avec la décomposition en facteurs premiers).
C'est absurde car en contradiction avec l'hypothèse p divise a^m.

Après je peux comprendre que recourir à la décomp. en fact. premiers peut sembler alambiqué pour un exercice qui se fait avec des outils plus élémentaires... mais dès que je peux, j'utilise cette méthode car elle se "voit" bien je trouve. Mais bon c'est juste mon point de vue.

Par contre je me souviens d'un sujet de concours que j'avais totalement raté en voulant à tout prix utiliser cette décomposition. Alors qu'il fallait utiliser le "théorème Chinois des restes" (traduit avec un isomorphisme entre (Z/nZ)x(Z/mZ) et (Z/nmZ). Depuis je relativise un peu son efficacité (et la mienne également!) !

Bye !

[leon1789]

Tu pars de p divise a^m.

Tu supposes que p ne divise pas a (raisonnement par l'absurde).

Tu fais un raisonnement par l'absurde et la décomposition en facteurs premiers dans l'hérédité du raisonnement par récurrence, c'est ça ?... c'est compliqué !

Je propose une simple preuve par récurrence de : p | a^m => p | a

m=1 : ok

supposons et montrons

p | a^(m+1) = a^m . a
donc p | a^m ou p |a (car p premier)
donc p | a ( car H_m) ou p | a
donc p | a
d'où

[fourize]

(raisonnement par l'absurde). !

ah, oui ça marche et merci pour votre aide.
je tiens egalement à remercier tous qui ont participer à cette discussion.

[Lemniscate]

leon je ne fais PAS de récurrence ! Je pense qu'on peut s'en passer ici. (Sinon ma méthode serait vraiment trop compliquée !).