Calcul dérivée f' de f
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bartounet
- Messages: 7
- Enregistré le: 26 Juil 2007, 09:44
-
 par Bartounet » 27 Nov 2007, 20:54
par Bartounet » 27 Nov 2007, 20:54
Bonjour.
Je suis confronté à un exercice sur lequel je bloque à cause d'une dérivée.
Voici l'énoncée :
On considère la fonction f définie sur l'intervalle [1,10] par : f(x) = x -6 + 4/x
Je dois calculer la dérivée f' de f, et montrer que pour tout x de [1,10], f'(x) = (x-2)(x+2)/x²
Merci de bien vouloir me donner un coup de main pour calculer la dérivée f' de f, et ensuite m'aider à montrer ce qui est demandé, je ne m'en sors vraiment pas :help:
-
Noemi
- Membre Complexe
- Messages: 3241
- Enregistré le: 20 Oct 2007, 16:09
-
 par Noemi » 27 Nov 2007, 20:58
par Noemi » 27 Nov 2007, 20:58
La dérivée de x-6 : forme ax+b donc 1
La dérivée de 4/x forme a/v soit -4/x^2
Il faut ensuite réduire au même dénominateur et factoriser
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 27 Nov 2007, 21:02
par Babe » 27 Nov 2007, 21:02

tu reconnait a^2-b^2=(a-b)(a+b)
d'où
(x+2)}{x^2})
-
Bartounet
- Messages: 7
- Enregistré le: 26 Juil 2007, 09:44
-
 par Bartounet » 27 Nov 2007, 21:18
par Bartounet » 27 Nov 2007, 21:18
Merci à vous.
Pour montrer que f'(x) = (x-2)(x+2)/x², il suffit de dire que c'est de la forme a^2-b^2=(a-b)(a+b) ? Ca suffit à le montrer ?
-
Bartounet
- Messages: 7
- Enregistré le: 26 Juil 2007, 09:44
-
 par Bartounet » 27 Nov 2007, 21:48
par Bartounet » 27 Nov 2007, 21:48
De plus je n'arrive pas à factoriser :mur:
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 27 Nov 2007, 21:52
par Babe » 27 Nov 2007, 21:52
Babe a écrit:
tu reconnait a^2-b^2=(a-b)(a+b)
d'où
(x+2)}{x^2})
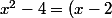(x+2))
-
Bartounet
- Messages: 7
- Enregistré le: 26 Juil 2007, 09:44
-
 par Bartounet » 27 Nov 2007, 22:31
par Bartounet » 27 Nov 2007, 22:31
C'est bon j'ai compris ! Merci de votre aide ! :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
