Polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 18 Oct 2007, 08:34
par ice456 » 18 Oct 2007, 08:34
Bonjour,
je suis bloqué pour démarer l'exercice.
Voici le contexte : on a un polynome

(x) de degré 2.
Son graphe passe par les points (0,h) et (1,0) et sa dérivée en x = 0 est nulle.
On note
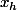
le point fixe de

: [0,1]

[0,1].
Il nous est demandé de donner une formule pour
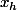
en fonction de h dans l'interval [0,1]
Je ne vois pas trop comment faire...
Comme
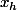
est un point fixe on a

(
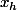
) =
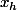
mais ensuite? :hum:
Merci de votre aide

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 18 Oct 2007, 08:52
par chan79 » 18 Oct 2007, 08:52
bonjour
Ph est bien un polynôme de degré 2
alors Ph(x)=a(h)x²+b(h)x+c(h)
essaie de commencer par trouver a(h), b(h) et c(h) en fonction de h avec les données du début
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 18 Oct 2007, 12:51
par ice456 » 18 Oct 2007, 12:51
J'ai trouvé que a = -h ; b = 0 et c = h.
Donc on peut réécrire

(x) = -h x² + h
Ensuite pour donner une formle pour
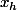
en focntion de h il faut utilisé la définition de point fixe c'est ça?
On aurait donc par définition du point fixe que
)
=
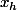
et donc -h x² + h = x et en isolant x on a la formule c'est ça?
Merci d'avance
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 18 Oct 2007, 14:29
par ice456 » 18 Oct 2007, 14:29
J'ai trouvé que a = -h ; b = 0 et c = h.
Donc on peut réécrire

(x) = -h x² + h
Ensuite pour donner une formle pour
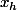
en focntion de h il faut utilisé la définition de point fixe c'est ça?
On aurait donc par définition du point fixe que
)
=
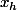
et donc -h x² + h = x et en isolant x on a la formule c'est ça?
Merci d'avance
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 18 Oct 2007, 16:48
par ice456 » 18 Oct 2007, 16:48
J'ai trouvé que a = -h ; b = 0 et c = h.
Donc on peut réécrire

(x) = -h x² + h
Ensuite pour donner une formle pour
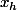
en focntion de h il faut utilisé la définition de point fixe c'est ça?
On aurait donc par définition du point fixe que
)
=
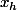
et donc -h x² + h = x et en isolant x on a la formule c'est ça?
Merci d'avance
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 18 Oct 2007, 19:25
par ice456 » 18 Oct 2007, 19:25
J'ai trouvé que a = -h ; b = 0 et c = h.
Donc on peut réécrire

(x) = -h x² + h
Ensuite pour donner une formle pour
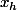
en focntion de h il faut utilisé la définition de point fixe c'est ça?
On aurait donc par définition du point fixe que
)
=
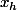
et donc -h x² + h = x et en isolant x on a la formule c'est ça?
Merci d'avance
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 18 Oct 2007, 20:28
par ice456 » 18 Oct 2007, 20:28
Mon raisonnement est-il correct?
-
Help
- Membre Naturel
- Messages: 53
- Enregistré le: 22 Aoû 2006, 12:54
-
 par Help » 18 Oct 2007, 20:49
par Help » 18 Oct 2007, 20:49
Oui, c'est ça
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 20 Oct 2007, 09:33
par ice456 » 20 Oct 2007, 09:33
Bonjour à tous,
j'aimerai avoir des précisions concernant la question :
Pour résumé j'ai donc trouvé que

(x) = -h x² + h
J'utilise donc le point fixe pour trouver l'expression à savoir x = -h x² + h
Je résoud alors -hx² - x + h = 0 et je trouve

Et donc mon expression

c'est mon
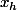
?
J'ai un peu de mal avec la notion de point fixe je dois avouer lol
J'aurais une autre question par la suite mais je préfère être sur que la base soit bonne avant de continué
Merci pour votre aide
-
Cygnusx1
- Membre Naturel
- Messages: 44
- Enregistré le: 08 Juil 2007, 21:48
-
 par Cygnusx1 » 20 Oct 2007, 09:38
par Cygnusx1 » 20 Oct 2007, 09:38
Il ne reste plus qu'a vérifier lequel des 2 racines de ton polynome est bien dans l'intervalle demandée et tu auras fini :)
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 20 Oct 2007, 10:03
par ice456 » 20 Oct 2007, 10:03
Ok merci bcp
J'ai donc testé avec les différentes valeurs de h

[0,1] et j'ai trouver que c'était l'expression

qui reste dans l'inteveral [0,1].
La question suivante maintenant lol
On nous demande de tester de manière graphique la converge de la méthode du point fixe sur le polynome

(x) pour divers valeurs de h.
J'ai un peu de mal à comprendre ceci
quand on parle de méthode du point fixe on fait référence à l'expression
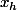
?
Et si c'est le cas je dois donc appliqué

(
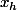
) = -h
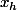
² + h ?
Merci pour l'aide:)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 20 Oct 2007, 10:11
par Joker62 » 20 Oct 2007, 10:11
La méthode du point fixe consiste à créer une suite récurrente, comme expliqué dans le post précédent.
On pose x_(n+1) = f(x_n).
Donc c'est quoi le principe !
On choisit un point de [0;1], on le projette vecticalement sur la courbe de f, on le projette horizontalement sur la courbe y = x, et on obtient ainsi un point de coordonnées (x_n+1, f(x_n)), on recommence le procésus, on s'aperçoit que ça converge vers le point fixe :) ( si f contractante )
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 20 Oct 2007, 12:24
par ice456 » 20 Oct 2007, 12:24
Ok merci pour l'explication
Donc dans ce cas si il faut faire

(

) =

où alors je suis completement à coté? lol
J'essaye avec h = 1 mon polynome devient donc

(x) = -1x² + 1
Pour le

=0, a donc

(

) = 1 =

Ensuite on continue donc

(

) = 0 et là on va tourner en rond à chaque passage :hum:
J'ai comme une forte impression que je me trompe :we:
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 20 Oct 2007, 13:59
par ice456 » 20 Oct 2007, 13:59
Ok merci pour l'explication
Donc dans ce cas si il faut faire

(

) =

où alors je suis completement à coté? lol
J'essaye avec h = 1 mon polynome devient donc

(x) = -1x² + 1
Pour le

=0, a donc

(

) = 1 =

Ensuite on continue donc

(

) = 0 et là on va tourner en rond à chaque passage :hum:
J'ai comme une forte impression que je me trompe :we:
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 20 Oct 2007, 14:58
par ice456 » 20 Oct 2007, 14:58
Ok merci pour l'explication
Donc dans ce cas si il faut faire

(

) =

où alors je suis completement à coté? lol
J'essaye avec h = 1 mon polynome devient donc

(x) = -1x² + 1
Pour le

=0, a donc

(

) = 1 =

Ensuite on continue donc

(

) = 0 et là on va tourner en rond à chaque passage :hum:
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 20 Oct 2007, 17:05
par ice456 » 20 Oct 2007, 17:05
Ok merci pour l'explication
Donc dans ce cas si il faut faire

(

) =

où alors je suis completement à coté? lol
J'essaye avec h = 1 mon polynome devient donc

(x) = -1x² + 1
Pour le

=0, a donc

(

) = 1 =

Ensuite on continue donc

(

) = 0 et là on va tourner en rond à chaque passage :hum:
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 21 Oct 2007, 09:38
par ice456 » 21 Oct 2007, 09:38
Ok merci pour l'explication
Donc dans ce cas si il faut faire

(

) =

où alors je suis completement à coté? lol
J'essaye avec h = 1 mon polynome devient donc

(x) = -1x² + 1
Pour le

=0, a donc

(

) = 1 =

Ensuite on continue donc

(

) = 0 et là on va tourner en rond à chaque passage :hum:
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 21 Oct 2007, 11:51
par ice456 » 21 Oct 2007, 11:51
Ok merci pour l'explication
Donc dans ce cas si il faut faire

(

) =

où alors je suis completement à coté? lol
J'essaye avec h = 1 mon polynome devient donc

(x) = -1x² + 1
Pour le

=0, a donc

(

) = 1 =

Ensuite on continue donc

(

) = 0 et là on va tourner en rond à chaque passage :hum:
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 21 Oct 2007, 13:22
par ice456 » 21 Oct 2007, 13:22
J'ai fait le graphe de la manière suivante et j'obtient quasi une ligne droite c'est normal? :hum:
J'ai testé avec h = 0,5 ; 0,1 et 0,2
Je m'attendais plus a quelque chose qui varie puis se stabilise vers le point fixe au fure et à masure que la suite avance
quelqu'un pourrait-il m'aider?
Merci d'avance
-
ice456
- Membre Relatif
- Messages: 109
- Enregistré le: 13 Oct 2007, 14:43
-
 par ice456 » 21 Oct 2007, 14:31
par ice456 » 21 Oct 2007, 14:31
J'ai fait le graphe de la manière suivante et j'obtient quasi une ligne droite c'est normal? :hum:
J'ai testé avec h = 0,5 ; 0,1 et 0,2
Je m'attendais plus a quelque chose qui varie puis se stabilise vers le point fixe au fure et à masure que la suite avance
quelqu'un pourrait-il m'aider?
Merci d'avance
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
