Espaces Vectoriels

[sl4cker]

Voila j'ai du mal à résoudre cet eercice si quelqu'un pouvait m'aider, merci d'avance :

On considère E = R^4 et les vecteurs :

u = (1,1,0,-1)
v = (1,0,0,-1)
w = (2,1,0,-1)

On note F = Vect(u,v,w)
et G = {(x,y,z,t) appartient à E | x + y - z + 2t = 0 }

1. Montrer que F et G qont 2 sous espacs vectoriels de E
2. Determiner F [INTER] G
3. La somme F+G est-elle directe ?
4. F et G sont ils des sous ensembles supplémentaires de E ?

[mathelot]

1.
F par définition. L'ensemble des combinaisons linéaires de 3 vecteurs est un e.v
G est un sous espace vectoriel comme noyau d'une forme linéaire.

2.
Sais tu montrer que dim(F)=3 ?
Il faut exhiber un déterminant mineur 3x3 non nul à partir des coordonnées
de.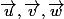
G est un hyperplan, de dimension 3.
n'est pas réduit à

pour déterminer , je considèrerai un vecteur
Comme un déterminant mineur d'ordre 3 est non nul, ça permet
de calculer les coeff a,b,c en fonction des coordonnées x,y,t de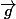
Ensuite , en exprimant que
ça donne une relation entre a,b et c et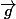 est alors combinaison linéaire de seulement deux vecteurs.

3.
La somme n'est donc pas directe
4.
a fortiori, F et G ne sont pas supplémentaires.


PS: il y a aussi le thm :

[sl4cker]

Je n'ai pas tout compris mais merci quand même :we:

[mathelot]

comment ferais tu ?

[sl4cker]

Il faudrait faire sans les notions d'hyperplan et (dim) car je ne lai pas encore vu en cours :D

[mathelot]

pour la question (2), prendre un vecteur quelconque (4 coord. x,y,z,t) de
exprime que est combinaison linéaire de u,v,w
avec des coefficients a,b,c.

Pourquoi est-ce que l'on peut calculer a,b,c en fonction de x,y,t ?