Polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 07 Jan 2007, 09:59
par dragonmaster » 07 Jan 2007, 09:59
Soit f(x) est une polynôme . f(x) a 2006 racines distincts et deg(f) = 2006 . Montrez que le longueur des racines de l'inéqualité suivant est moins que 1.
}{f(x)} > 2007)
-
manu18ck
- Membre Relatif
- Messages: 112
- Enregistré le: 18 Nov 2006, 11:58
-
 par manu18ck » 07 Jan 2007, 14:31
par manu18ck » 07 Jan 2007, 14:31
dragonmaster a écrit:Soit f(x) est une polynôme . f(x) a 2006 racines distincts et deg(f) = 2006 . Montrez que le longueur des racines de l'inéqualité suivant est moins que 1.
}{f(x)} > 2007)
c koi "le longueur des racines"??
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 07 Jan 2007, 15:21
par dragonmaster » 07 Jan 2007, 15:21
Par exemple : les racines est ]a , b [ , et |a - b| est le longueur .
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2007, 18:20
par yos » 07 Jan 2007, 18:20
L'inégalité équivaut à la suivante :
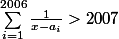
.
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 07 Jan 2007, 19:21
par dragonmaster » 07 Jan 2007, 19:21
D'accord . Mais c'est pas fini .
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 07 Jan 2007, 20:39
par fahr451 » 07 Jan 2007, 20:39
qu'appelle - t-on racine d'une inégalité?
je ne connais que les racines d'une équation algébrique ou les solution d'une équation.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2007, 21:08
par yos » 07 Jan 2007, 21:08
J'imagine qu'il parle de l'ensemble de solutions de l'inéquation
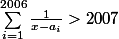
(d'inconnue x).
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 07 Jan 2007, 21:30
par dragonmaster » 07 Jan 2007, 21:30
Oui .Le longueur des racines , c'est le longueur sur l'axe Ox .
-
mathelot
 par mathelot » 07 Jan 2007, 21:34
par mathelot » 07 Jan 2007, 21:34
le diamètre de l'ensemble des racines.En regardant le comportement de la fonction
}{f(x)})
au voisinage des pôles, on voit très facilement que l'ensemble des solutions de l'inégalité a un diamètre

et plus de 2006 composantes connexes.
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 07 Jan 2007, 22:58
par dragonmaster » 07 Jan 2007, 22:58
Non , c'est pas ça ! L'inéqualité a beaucoup les racines , c'est les intervalles . Chaque intervalle a une longueur . La demande ici est montrer que le longueur totale est moins que 1 .
Je pense que le problème est vraie , parce que je déjà fini .
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 08 Jan 2007, 01:16
par darkmaster » 08 Jan 2007, 01:16
:hum: :hum: :hum: :hum: :hum: une classique
=\displaystyle{\sum_{i=1}^{2006}}\frac{1}{x-a_i}-2007)
;
On a g'(x)>0 alors f est décroissante. Apres un peu d'étude ondoit avoir que g possède 2006 racines

.

. t_{2006} \in ]a_{2006},+\infty[. Et on doit calculer
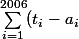.)
On a bien

Donc
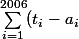 <\frac{2006}{2007}<1)
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 01:37
par dragonmaster » 08 Jan 2007, 01:37
Pourquoi calculer
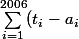)
?
Pourquoi on a bien

?
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 01:47
par dragonmaster » 08 Jan 2007, 01:47
Je comprends que les racines sont
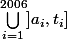
. Mais

, je n'est pas sûre .
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 08 Jan 2007, 01:55
par amine801 » 08 Jan 2007, 01:55
je vois que les master s'asemble je vous lesse lol :w
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 08 Jan 2007, 02:13
par darkmaster » 08 Jan 2007, 02:13
dragonmaster a écrit:Je comprends que les racines sont
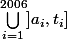
. Mais

, je n'est pas sûre .
Et oui, quelque fois j'oublie la solution; mais ce problème est bien un d'olympiades internationals. La solution officielle est qu'on écrire
-(a_1+a_2+...+a_n))
On peut calculer tous les deux sommes par la théorème de Viette.
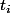
est racine de g(x) et

est racine de f(x). Après on peut démontrer facilement que la somme des intervals est inférieur que 1. (je veux pas préciser tout ça , je te laisse de finir)
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 02:27
par dragonmaster » 08 Jan 2007, 02:27
Montrer

avec

n'est pas simple . Je ne sais pas que cette problème est d'olympiades internationals . Je bien sûr que ma solution est spéciale .
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 08 Jan 2007, 02:31
par darkmaster » 08 Jan 2007, 02:31
dragonmaster a écrit:Montrer

avec

n'est pas simple . Je ne sais pas que cette problème est d'olympiades internationals . Je bien sûr que ma solution est spéciale .
C'est pas simple parce que c'est faux. Tous on peut faire c'est qu'on fait comme la solution officielle. C'est tout.
-
dragonmaster
- Membre Naturel
- Messages: 23
- Enregistré le: 29 Déc 2006, 02:20
-
 par dragonmaster » 08 Jan 2007, 03:35
par dragonmaster » 08 Jan 2007, 03:35
C'est ma repond
 = \displaystyle{\prod _{i=1}^{2006} }(x - a_i))
Supposé que

avec i > j . Si il existe 2 numéro

tel que
 >1000)
et
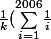 x <br />On a la polynôme [Tex] \ f(x) = \displaystyle{\prod _{i=1}^{2006}} (x - a_i))
avec

 = \frac {f(x)}{f'(x)} = \displaystyle{\sum _{i=1}^{2006}}\frac {1}{x - a _i})
g(x) est décroissante sur chaque intervalle
)
.
Les numéros à gauche de a1 n'est pas les racines . On travaille avec l'intervalle à droite

.
À point

:
Posez
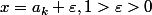
, alors :
= (\displaystyle{\sum _{i=1}^{2006}}\frac {1}{x - a _i} ) - \frac{1}{x - a _k} h(x) décroissante ( entrer 2 numéros a _k et a _k+1 )<br />alors , il faut que [tex] \frac{1}{x - a _k} > 2006 \Rightarrow \varepsilon 2007)
a la longueur totale qui est moins que 1 . Il est équivalent avec :
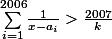
(1)
La longueur de (1) est moins que 1
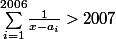
(2)
ainsi que l'ensemble des racines de (2) est une parte de l'ensemble des racines de (1) . Maintenant , c'est fini !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
}{f(x)} > 2007)
. Mais
, je n'est pas sûre .
 = \displaystyle{\prod _{i=1}^{2006} }(x - a_i))
 avec i > j . Si il existe 2 numéro
avec i > j . Si il existe 2 numéro  tel que
tel que  >1000) et
et 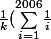 x <br />On a la polynôme [Tex] \ f(x) = \displaystyle{\prod _{i=1}^{2006}} (x - a_i)) avec
avec 
 = \frac {f(x)}{f'(x)} = \displaystyle{\sum _{i=1}^{2006}}\frac {1}{x - a _i})
) .
. .
. :
: 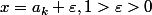 , alors :
, alors := (\displaystyle{\sum _{i=1}^{2006}}\frac {1}{x - a _i} ) - \frac{1}{x - a _k} h(x) décroissante ( entrer 2 numéros a _k et a _k+1 )<br />alors , il faut que [tex] \frac{1}{x - a _k} > 2006 \Rightarrow \varepsilon 2007) a la longueur totale qui est moins que 1 . Il est équivalent avec :
a la longueur totale qui est moins que 1 . Il est équivalent avec :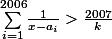 (1)
(1)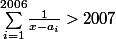 (2)
(2)