Equation modulaire

[blaidddrwg]

Bonjour la communauté,

Je cherche à savoir comment on peut résoudre l'équation suivante :

3=(3^2^(x mod 110)) mod 253.

Je précise que x appartient à l'ensemble Z, je cherche par pure curiosité

En vous remerciant pour votre aide,

Bon dimanche,

[Ben314]

Salut,
C'est pas très clair ton truc. Ce que je crois comprendre :
- On part d'un entier .
- On regarde le reste de la division euclidienne de par .
- On calcule (*)
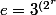- On veut que soit congru à modulo

C'est ça ?

Si oui, il n'y a pas de difficulté, c'est juste un peu chiant vu la taille des nombres :
On commence par résoudre qui donne une/des congruence(s) pour modulo un certain puis on résous .

(*) La fonction puissance n'est pas associative donc sans parenthèse, ni précision concernant la notation dans le laïus, c'est jamais clair ce que ça signifie.