Espaces vectoriels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
par bitonio » 30 Nov 2006, 19:57
Bonjour à tous,
j'ai encore un peu de mal avec un court assez frais
Soit F l'ensemble des matrices de la forme
)
, a et b des rééls
Montrer que F est un sev de (
,+,x))
*Je commence par dire que
)
(
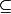
=inclu je n'ai pas trouvé la commande ...)
*Ensuite 0 J
*Enfin il faut montrer que c'est stable par combinaison linéaire... C'est la que je coince un peu
Merci d'avance!
Ciao
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
par tize » 30 Nov 2006, 20:12
Il te suffit de prendre deux matrices
)
et
)
et deux réels
et
et montrer que :
+\beta\(\begin{array}{ccc}c&-d\\d&c\end{array}\)\in F)
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
par bitonio » 30 Nov 2006, 20:40
merci bien ;) effectivement c'est vraiment pas compliqué
-
bitonio
- Membre Rationnel
- Messages: 764
- Enregistré le: 28 Mai 2006, 15:29
-
par bitonio » 30 Nov 2006, 20:56
Autre question au passage. Peux on expliciter une base ? je dirais bien sûr oui... mais je ne vois pas quelle base choisir...
-
Gato
- Membre Naturel
- Messages: 74
- Enregistré le: 17 Nov 2006, 21:56
-
par Gato » 30 Nov 2006, 21:25
Hello,
tu peux exprimer toute matrice de F sous la forme :
M=aA+bB ; A et B étant deux matrices indépendantes.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
