Séries

[Jota]

Salut, je n'arrive pas a faire la question de 2 de l'exercice suivant:
Soit la fonction 2 - périodique définie par .
1- Calculer les coefficients de Fourier trigonométriques de f.
2- En déduire la valeur de la somme .

J'ai trouvé a la question 1) et . Et c'est la déduction qui me pose problème.

Merci d'avance.

[pascal16]

je ne sais pas si ça peut aider
cos(n*pi/2)
->1 si n=4p
-> -1 si n= 4p+2
-> 0 si n = 4p+1 ou 4p+3

[Rdvn]

Bonjour
Reprenez vos calculs en considérant cette fois ci que f est Pi-périodique (et paire, comme déjà remarqué),
le lien avec la question 2 est alors bien plus clair (je n'ai pas vérifié votre calcul, à priori il semble correct, mais c'est la présentation des coefficients qui fait obstacle à la question 2 , lorsque vous partez de f 2Pi-périodique)
Bon courage

[aviateur]

Bonjour
Y a rien qui te choque dans ta réponse?
D'autre part, une fois qu'on a les bons coefficients de Fourier la réponse à la deuxième question est évidente,
si on sait ce qu'est la série de Fourier d'une fonction, en l'occurrence ici f(x)=|cos(x)|.
ça doit venir à l'esprit tout de même d'écrire le résultat fondamental du cours.

[Jota]

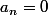
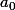
Salut, pour n pair, on a: et pour n impair, on a: . Pour pouvoir ecrire la serie de fourier, on va gérer le cas de comment?

[aviateur]

Et pour n=1. a_n=????
on va gérer comment? et pour n=1, a_n te pose pas de problème?
Mais d'abord répond aux questions.
Est ce que tu peux écrire ce que dit ton cours?

[Rdvn]

Bonjour à tous
Désolé pour l'étourderie que je n'avais pas relevée (en fait je n'ai repris que le 2), il est clair que Aviateur a raison, et que n=1 était à traiter à part si on considère f 2Pi-périodique. Tout devient plus clair si on considère
f Pi-périodique, c'est en cela qu'il me semblait intéressant de suggérer à Jota une autre piste , à présent il lui reste la question posée par Aviateur ...

[Jota]

La série de Fourier de f va s'écrire .

[aviateur]

Rebonjour
Bon on avance mais c'est pas encore ça. C'est cos(2nx) ?????

Mais surtout le cours permet de te dire dans quel cas tu as Une fois que tu auras écris cela
tu verras que la question 2. est évidente.

Donc le premier problème est de corriger ta série de Fourier.

[Jota]

OK, merci beaucoup!!