Soit n >= 2 un nombre de carmichael on souhaite demontrer que n n'est divisible par le carre d'aucun entier premier pour cela on raisonne en absurde en posant n =qp^2 avec p premier on pose a =pq+1
1- montrer que a^(n-1) est congru a 1 modulo n(pas de soucis je l'ai deja demontre )
2 - montrer que p est l'ordre de a modulo n . Conclure
(on dit que r est l'ordre de k modulo m si pour tout i de N k^i est congru à 1 modulo m ssi r/i )
J'ai besoi d'aide pour la question 2 svp et merci d'avance
Re: arithmetique
3 messages
- Page 1 sur 1
Re: arithmetique
Salut,
Le calcul de l'ordre de dans
dans ^*) , c'est simple vu que pour tout entier naturel
, c'est simple vu que pour tout entier naturel  , on a
, on a 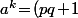^k\!=\!\sum_{i=0}^k{k\choose i}(pq)^i\!\equiv\!kpq\!+\!1\ [n]) vu que
vu que ^i\!\equiv\!0\ [n]) pour tout
pour tout  .
.
Le calcul de l'ordre de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: arithmetique
Ben314 a écrit:Salut,
Le calcul de l'ordre dedans
, c'est simple vu que pour tout entier naturel
, on a
vu que
pour tout
.
En fait oui merci , mais je ne comprends pas vraiment comment demontrer que p est l'ordre de a modulo n est ce que je dois utiliser une double implication ? Vu que cette notion d'ordre est nouvelle pour moi et merci d'avance
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
