Bonjours , je suis en terminal S et je n'arrive pas à faire cet exercice:
Pour tout entier naturel n, on pose :
fn(x)= e^(-nx)/(1+e^(-x))
et
un = (integrale de borne 0 et 1) fn(x) dx
1. Calculer U1.
2. Démontrer que U0+U1=1, en déduire U0.
3. Démontrerque,pourtoutentiern:
0 ≤ Un ≤ (integrale de borne 0 et 1) e^(-nx) dx
4.Déduire de la question précédente que la suite (Un) est convergente, et calculer sa limite.
j'ai essayer de résoudre U1 mais j'arrive pas à faire les primitives des ln
Voila mon problème, merci beaucoup de m'aider
Primitives ln
10 messages
- Page 1 sur 1
Re: primitives ln
salut
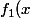 = \dfrac {e^{-x}}{1 + e^{-x}}) est presque de la forme u'/u ...
est presque de la forme u'/u ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: primitives ln
c'est ce que javais fait mais je n'ai pas trouvé ca sur la calculatrice
ce que j'ai fait :
f(x)= e^(-x)/(1+e^(-x)) avec ln(U)' = U'/U
F(x)= ln(1+e^(-x))
avec des calcule au final pour U1= ln((1+e^(-1))/2)
ce que j'ai fait :
f(x)= e^(-x)/(1+e^(-x)) avec ln(U)' = U'/U
F(x)= ln(1+e^(-x))
avec des calcule au final pour U1= ln((1+e^(-1))/2)
Re: primitives ln
Sinon, tu as ce site (qui est en anglais par contre) qui te permet d'entrer le calcul que tu veux, et il te donne la réponse, et il y a un mode pas à pas dans lequel tu peux voir toutes les étapes :
http://www.wolframalpha.com
http://www.wolframalpha.com
Re: primitives ln
zygomatique a écrit:salutest presque de la forme u'/u ...
il est peut-être temps de te mettre au boulot sérieusement !!!
qui est u ? donc u' ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: primitives ln
fn(x)=e^(-nx)/(1+e^(-x))
e^(-nx) est positif
(1+e^(-x)) est plus grand que 1 et est positif.
par croissance de l'intégrale on a la 3.
pour trouver une primitive de e^(-nx) à la main, on dérive e^(-nx) et on corrige
e^(-nx) est positif
(1+e^(-x)) est plus grand que 1 et est positif.
par croissance de l'intégrale on a la 3.
pour trouver une primitive de e^(-nx) à la main, on dérive e^(-nx) et on corrige
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
