Primitives, les bases :*:
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 17:14
par J-R » 11 Aoû 2007, 17:14
bonsoir,
je suis en train de voir les primitives et j'aimerais savoir les méthodes de calcul, les astuces aussi...
exemple: déterminer une primitive de
=(2x+1)(x^2+x-7)^3)
.
merci

-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 17:16
par anima » 11 Aoû 2007, 17:16
J-R a écrit:bonsoir,
je suis en train de voir les primitives et j'aimerais savoir les méthodes de calcul, les astuces aussi...
exemple: déterminer une primitive de
=(2x+1)(x^2+x-7)^3)
.
merci

Y'a rien de plus simple. Ne vois-tu pas que (2x+1) est la dérivée de (x^2+x-7)? Des lors, on a
 = u' u^3)
.
Et
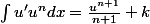
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 17:26
par J-R » 11 Aoû 2007, 17:26
Des lors, on a f(x) = u' u^3
d'accord mais après:
Et
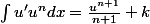
là faut m'expliquer ou me donner un nain dix.
(je sais que
dx=F(b)-F(a))
)
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 17:27
par J-R » 11 Aoû 2007, 17:27
sinon si vous avez des exos d'entrainement...
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 17:30
par anima » 11 Aoû 2007, 17:30
J-R a écrit:sinon si vous avez des exos d'entrainement...
Tu as demandé une primitive, donc une intégrale non-bornée.
Une primitive, une fois derivée, redonne la fonction normale. u^{n+1}/(n+1) est-elle la primitive de u' u^{n}? On vérifie:
dx} = \frac{1}{n+1} (n+1)u'u^{n} = u' u^n)
Prouvé :ptdr:
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 18:00
par J-R » 11 Aoû 2007, 18:00
d'accord j'ai compris le calcul de la dérivée.
je vais essayer de m'entrainer et je reviendrais surement
merci :)
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 18:35
par J-R » 11 Aoû 2007, 18:35
les problèmes commencent, je reviens as ton calcul de :
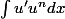
, comment as tu fais pour retomber sur

merci
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 11 Aoû 2007, 19:21
par Babe » 11 Aoû 2007, 19:21
J-R a écrit:exemple: déterminer une primitive de
=(2x+1)(x^2+x-7)^3)
.
ou alors si tu veux pas reflechir, tu developpe et il n'y a plus qu'à integrer betement
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 19:23
par anima » 11 Aoû 2007, 19:23
Babe a écrit:ou alors si tu veux pas reflechir, tu developpe et il n'y a plus qu'à integrer betement
Un calcul ne s'effectue pas, il se médite.
@J-R: une primitive, une fois dérivée, donne la fonction initiale...
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 19:28
par J-R » 11 Aoû 2007, 19:28
babe: ouais ok
sinon pour ma question sur le calcul de l'intégrale ?
merci
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 19:38
par anima » 11 Aoû 2007, 19:38
J-R a écrit:babe: ouais ok
sinon pour ma question sur le calcul de l'intégrale ?
merci
Tu n'as pas donné les bornes s'il y en a.
Sinon, ta primitive vaut
^4}{4})
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 19:53
par J-R » 11 Aoû 2007, 19:53
j'ai fait ma primitive mais je voulais revenir sur ton calcul :
comment fais tu pour partir de l'intégrale et arriver au second membre ? (parce que je ne sais faire que dans l'autre sens ...)
merci
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 19:55
par anima » 11 Aoû 2007, 19:55
J-R a écrit:j'ai fait ma primitive mais je voulais revenir sur ton calcul :
comment fais tu pour partir de l'intégrale et arriver au second membre ? (parce que je ne sais faire que dans l'autre sens ...)
merci
Attention, c'est prouvé dans l'autre sens.
)
, une fois dérivé, donne u' * u^n. Donc, u' * u^n une fois intégré donne u^{n+1}/(n+1) a une constante pres.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 11 Aoû 2007, 19:56
par lapras » 11 Aoû 2007, 19:56
salut Anima, comment obtient on la constante d'intrégration?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 19:59
par anima » 11 Aoû 2007, 19:59
lapras a écrit:salut Anima, comment obtient on la constante d'intrégration?
Notre petit copain n'a pas précisé ni de bornes, ni de conditions...donc, on ne l'obtient pas!
De plus, il a dit "une primitive". Dans ce cas, prenons k=0 pour se simplifier la vie! :we:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 11 Aoû 2007, 20:01
par lapras » 11 Aoû 2007, 20:01
Ok.
Mais si il avait donné les conditions necessaires, comment faire ?
Si je comprend bien les intégrales s'obtiennent en utilisant un tableau de primitives usuelles ?
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 20:11
par J-R » 11 Aoû 2007, 20:11
anima: d'accord on est obligé de partir dans l'autre sens. Mais alors quelle est la méthode pour intégrer
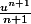
?
merci
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 11 Aoû 2007, 20:13
par anima » 11 Aoû 2007, 20:13
J-R a écrit:anima: d'accord on est obligé de partir dans l'autre sens. Mais alors quelle est la méthode pour intégrer
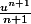
?
merci
Dériver, pas intégrer.
@lapras: On te donne en général une condition telle que F(0)=0 ou similaire. Il suffit de résoudre une équation a une inconnue :we:
-
J-R
- Membre Relatif
- Messages: 459
- Enregistré le: 26 Mai 2007, 18:34
-
 par J-R » 11 Aoû 2007, 20:16
par J-R » 11 Aoû 2007, 20:16
oui nan mais je sais dériver (en plus tu l'a fait plus haut) ca mais comment partir de
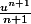
pour arriver à
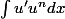
? puisqu'on ne peut pas dans l'autre sens....
merci
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 11 Aoû 2007, 20:21
par Sylar » 11 Aoû 2007, 20:21
Une primitive de :
u'.u^n c'est: u^(n+1) /(n+1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités