Arithmétique
9 messages
- Page 1 sur 1
Re: Arithmétique
Bonjour;
Soit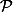 l'ensemble des nombres entiers naturels, et soit
l'ensemble des nombres entiers naturels, et soit 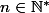 ,
,
donc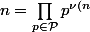} = \prod_{i=1}^r p_i^{k_i}) avec
avec 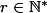 ,
, 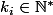 ,
, 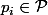 et
et  \in \mathbb N) ,
,
donc = n \prod_{i=1}^r (1 - \frac{1}{p_i})) ,
,
cette dernière formule vous permettra de conclure pour n pair et n impair .
Soit
donc
donc
cette dernière formule vous permettra de conclure pour n pair et n impair .
Re: Arithmétique
Bonjour;
soit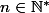 ,
,
si n est impair , on a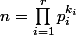 avec
avec 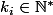 et
et  impair pour tout i ,
impair pour tout i ,
on a aussi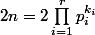 ,
,
donc = n \prod_{i=1}^r (1 - \frac{1}{p_i})) et
et  = 2 n (1 - \frac{1}{2}) \prod_{i=1}^r (1 - \frac{1}{p_i})) ,
,
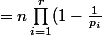 = \phi(n)) .
.
si n est pair, donc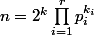 ou
ou 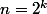 avec
avec 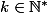 ,
, 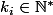 et
et  impair pour tout i,
impair pour tout i,
donc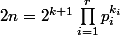 ou
ou 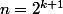 ,
,
donc = 2 n (1 - \frac{1}{2})\prod_{i=1}^r (1 - \frac{1}{p_i}) = 2 \phi(n)) ,
,
ou = \phi(2^{k+1}) = 2^{k+1}(1 - \frac{1}{2}) = 2*2^k (1 - \frac{1}{2}) = 2 \phi(2^k) = 2 \phi(n)) ,
,
donc pour n impair non nul on a toujours = 2 \phi(n)) ,
,
donc l'équation = \phi(2n)) s'avère pour n un nombre entier naturel impair .
s'avère pour n un nombre entier naturel impair .
soit
si n est impair , on a
on a aussi
donc
si n est pair, donc
donc
donc
ou
donc pour n impair non nul on a toujours
donc l'équation
Re: Arithmétique
salut
si on connaît quelques propriétés de l'indicatrice d'Euler (que je note f) (en fait une seule ici)
f est multiplicative : si n et m sont premiers entre eux alors f(mn) = f(m)f(n)
si n est impair alors :
2 et n sont premiers entre eux donc f(2n) = f(2)f(n)
or f(2) = 1 donc f(2n) = f(n)
réciproquement :
si f(2n) = f(n) alors :
f(2n) = f(2)f(n) => 2 et n sont premiers entre eux => n est impair
ou :
si n est pair alors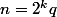 où 2 et q sont premiers entre eux
où 2 et q sont premiers entre eux
donc = f(2^k)f(q)) et
et  = f(2^{k + 1})f(q))
or \ne f(2^{k + 1})) donc
donc  \ne f(n))
...
si on connaît quelques propriétés de l'indicatrice d'Euler (que je note f) (en fait une seule ici)
f est multiplicative : si n et m sont premiers entre eux alors f(mn) = f(m)f(n)
si n est impair alors :
2 et n sont premiers entre eux donc f(2n) = f(2)f(n)
or f(2) = 1 donc f(2n) = f(n)
réciproquement :
si f(2n) = f(n) alors :
f(2n) = f(2)f(n) => 2 et n sont premiers entre eux => n est impair
ou :
si n est pair alors
donc
or
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Arithmétique
zygomatique a écrit:salut
si on connaît quelques propriétés de l'indicatrice d'Euler (que je note f) (en fait une seule ici)
f est multiplicative : si n et m sont premiers entre eux alors f(mn) = f(m)f(n)
si n est impair alors :
2 et n sont premiers entre eux donc f(2n) = f(2)f(n)
or f(2) = 1 donc f(2n) = f(n)
réciproquement :
si f(2n) = f(n) alors :
f(2n) = f(2)f(n) => 2 et n sont premiers entre eux => n est impair
ou :
si n est pair alorsoù 2 et q sont premiers entre eux
doncet
ordonc
...
Merci pour ta reponse , tu peux me donner le théorème qui dit " n et m sont premiers entre eux alors f(mn) = f(m)f(n)"
Re: Arithmétique
Bonjour,
le document suivant contient tout ce qu'il faut savoir sur l'indicatrice d'Euler, y compris le théorème demandé.
Bon courage.
le document suivant contient tout ce qu'il faut savoir sur l'indicatrice d'Euler, y compris le théorème demandé.
Bon courage.
Re: Arithmétique
aymanemaysae a écrit:Bonjour,
le document suivant contient tout ce qu'il faut savoir sur l'indicatrice d'Euler, y compris le théorème demandé.
Bon courage.
Merci beaucoup
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
