Bonsoir, j'ai un DM de Maths à faire pour mercredi et je bloque pour le faire. J'ai écrit les réponses que j'ai pu trouver. Pourrait-on m'aider ?
Voilà l'exercice :
Dans cet exercice, l'unité de longueur est le centimètre et x et h désignent des réels strictement positifs. On considère une boîte en forme de parallélépipède rectangle avec fond et couvercle à base carrée de côté x et dont la hauteur vaut h. On note respectivement v et s le volume et la surface totale de cette boîte.
1. Exprimer v puis s en fonction de x et h. En déduire la relation h=s/4x-x/2.
J'ai trouver V=hx² et S=4xh+2x² mais je n'ai pas trouvé pour le reste de la question.
2. Dans la suite de l'exercice, on suppose que la valeur de s est fixée.
a. Exprimer v en fonction de x et s
J'ai fait : V=s/4x-x^3/2
b. En étudiant les variations de la fonction v : x→v(x) sur ]0;+infini[, montrer que le volume v est maximal si, et seulement si, x= racine de s/6.
3. Établir que x= racine de s/6 si et seulement si h=x
4. Énoncer clairement la propriété démontré dans l'exercice.
DM dérivée
4 messages
- Page 1 sur 1
Re: DM dérivée
Bonjour Salomé,
1.
si s=2x²+4xh ===> extraire h :
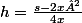 puis mettre chaque terme du numérateur sur 4x, donne :
puis mettre chaque terme du numérateur sur 4x, donne :
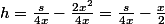
2a. je trouve :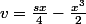
2b. }{4})
v(x) s'annule pour x=0 (exclu du Domaine d'Etude imposé) et pour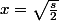
pour étudier les variations calculer la dérivée de v : = \frac{-6x^2 + s}{4}) :
:
===> Calculer la valeur pour laquelle la dérivée s'annule (c'est-à-dire la valeur pour laquelle on aura une tangente horizontale qui signifiera une valeur maximale de la courbe (car non point d'inflexion)), pour cela calculer le du numérateur puis la valeur. . .
du numérateur puis la valeur. . .
1.
si s=2x²+4xh ===> extraire h :
2a. je trouve :
2b.
v(x) s'annule pour x=0 (exclu du Domaine d'Etude imposé) et pour
pour étudier les variations calculer la dérivée de v :
===> Calculer la valeur pour laquelle la dérivée s'annule (c'est-à-dire la valeur pour laquelle on aura une tangente horizontale qui signifiera une valeur maximale de la courbe (car non point d'inflexion)), pour cela calculer le
Re: DM dérivée
Merci beaucoup pour l'aide j'ai fini le DM. J'avais un peu avancer aujourd'hui, et votre message m'a permis de le finir.
Encore merci.
Encore merci.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
