Derivabilité

[raninou]

Bonsoir,
Je suis en 1ère S
Est-ce que vous pouvez m'aider SVP ?
g(x) = (abs(x + 3) x - 3) / (x - 1)
Étudier la dérivabilité de g en -3
J 'ai essayé mais je n'ai pas pu
g'(x) = (2x + 3) / (x - 1)²

Merci d'avance.

[raninou]

Cas x+3≥0 et donc x≥−3 et x≠1 :

g(x) = (x² +3x - 3) / (x - 1)
g'(x) = (2x + 3) / (x - 1)²

Cas x+3≤0 et donc x≤−3 :
g(x) = (-x² - 3x - 3) / (x - 1)
g'(x) = (-2x - 3) / (x - 1)²

[Ben314]

Salut,
Peut-être que je me trompe, mais a mon avis, ce n'est pas ça qui est attendu, mais plutôt le fait que tu écrive que :
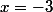est dérivable en si le rapport admet une limite lorsque tend vers -3.
Sauf que, pour étudier ce rapport, il faut que tu traite deux cas selon que x>-3 (et différent de 1) ou que x<-3 donc ça te fait deux "façons" de calculer la limite (on parle de "limite à droite" et de "limite à gauche").
Si ça donne le même résultat, c'est bon, g est dérivable en -3 et, sinon, c'est pas bon.