Dérivabilité d'une fonction sur un intervalle

[cnoby]

Bonjour,

Je ne comprend pas comment montrer qu'une fonction est dérivable sur un intervalle.
Le problème se pose notamment dans la question 1 de l'exercice ci dessous (que je dois faire en DM).




En résumé, je souhaite comprendre comment, de manière générale, démontrer qu'une fonction est dérivable dans un intervalle. je souhaite également comprendre comment montrer que cette fonction est dérivable avec les chiffres de l’énoncée.

PS : pour la question j'ai trouvé que si alors

D'avance je vous remercie,

S.H

[chan79]

PS : pour la question j'ai trouvé que si alors

D'avance je vous remercie,

S.H

Bonjour
Il s'agit sans doute de revenir à la définition de la dérivabilité.
Soit un réel a du domaine de définition
Tu vois si admet une limite quand tend vers .
Si elle existe, tu la nommes f'(a).

[Ben314]

Salut,
Normalement, ton cours doit contenir les définitions suivantes :
(a) Une fonction est dite dérivable en lorsque la limite existe.
Dans ce cas, la valeur de cette limite est appelée nombre dérivé de en et est notée .
(b) Une fonction est dite dérivable sur un intervalle lorsqu'elle est dérivable en tout .

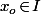
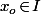
Donc, si tu n'avais que ces définitions là et rien de plus, il faudrait que tu vérifie que, pour tout , la limite existe (ce qui n'est pas particulièrement compliqué).

Sauf que ton cours contient non seulement des définitions, mais aussi des théorèmes (démontrés) qui disent en particulier que :
1) La somme de deux fonctions U et V dérivables est elle même dérivable et on a (U+V)'=U'+V'.
2) Le produit d'une fonctions U par un réel constant k est dérivable et on a (kU)'=kU'.
3) Le produit de deux fonctions U et V dérivables est lui même dérivable et on a (UxV)'=U'V+UV'.
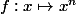
4) Pour tout entier naturel , la fonction est dérivable et on a
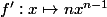
5) Toute fonction polynomiale est dérivable.

Donc ça te permet d'écrire sans te faire chier que ta fonction est dérivable vu qu'elle est polynomiale.

[cnoby]

Merci à tous !!!

je posterais mon DM dans l'après midi histoire de voire ce qui pourrait être améliorer.

@+