Séries
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
LeRozier
- Messages: 6
- Enregistré le: 28 Aoû 2015, 13:34
-
 par LeRozier » 28 Aoû 2015, 13:47
par LeRozier » 28 Aoû 2015, 13:47
Bonsoir,
Comment faire pour montrer que
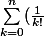 - (1+\frac{1}{n})^{n} = \sum_{k=2}^{n} \frac{1}{k!}[1-(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{k-1}{n})])
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Aoû 2015, 14:12
par arnaud32 » 28 Aoû 2015, 14:12
LeRozier a écrit:Bonsoir,
Comment faire pour montrer que
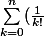 - (1+\frac{1}{n})^{n} = \sum_{k=2}^{n} \frac{1}{k!}[1-(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{k-1}{n})])
utilises le binome de newton
-
LeRozier
- Messages: 6
- Enregistré le: 28 Aoû 2015, 13:34
-
 par LeRozier » 28 Aoû 2015, 14:19
par LeRozier » 28 Aoû 2015, 14:19
C'est ce que j'avais commencé à faire, mais je reste bloqué ici :
)
-
LeRozier
- Messages: 6
- Enregistré le: 28 Aoû 2015, 13:34
-
 par LeRozier » 28 Aoû 2015, 14:22
par LeRozier » 28 Aoû 2015, 14:22
Je me suis débloqué jusqu'ici mais après je ne vois pas :
 * ... * n}{n^{k}}])
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Aoû 2015, 14:23
par arnaud32 » 28 Aoû 2015, 14:23
-
LeRozier
- Messages: 6
- Enregistré le: 28 Aoû 2015, 13:34
-
 par LeRozier » 28 Aoû 2015, 14:25
par LeRozier » 28 Aoû 2015, 14:25
Oui, c'est ce que j'ai mis plus haut.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Aoû 2015, 14:28
par arnaud32 » 28 Aoû 2015, 14:28
-
LeRozier
- Messages: 6
- Enregistré le: 28 Aoû 2015, 13:34
-
 par LeRozier » 28 Aoû 2015, 14:37
par LeRozier » 28 Aoû 2015, 14:37
Mais pourquoi k part de 2 et non de 0 ?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 28 Aoû 2015, 14:42
par arnaud32 » 28 Aoû 2015, 14:42
pour k=0 et k=1, ca vaut 0
-
LeRozier
- Messages: 6
- Enregistré le: 28 Aoû 2015, 13:34
-
 par LeRozier » 28 Aoû 2015, 14:44
par LeRozier » 28 Aoû 2015, 14:44
OK, merci .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
