Comparaison d'aire avec équation (dm)

[Effyy]

Bonjour à tous, j'aurais besoin de votre aide dans un de mes exercice de dm,voici l'énoncé:

Soit un rectangle de côté x et 2 cm. On construit sur deux de ses côtés consécutifs un triangle équilatéral. Lequel des trois polygones à le plus grand périmètre et pour quelle(s) valeur(s) de x?
Résoudre avec les outils les plus adaptés cet énoncé comparant des périmètres puis imaginer un énoncé de problème personnel relatif à une comparaison d'aires qui nécessite de résoudre une équation de second degré et résoudre ce problème.

La première partie j'ai réussit à la faire mais la deuxième partie avec les aires je sèche complètement, je me demandais déjà si je pouvais utiliser les périmètres que j'ai trouvé au début pour trouver les équations des aires ...aidez-moi s'il vous plait :help:

[Rizmoth]

Bonjour Effyy.

Si j'ai bien compris, dans la deuxième partie du problème, il s'agit d'abord de réécrire un énoncé. On peut essayer de modifier directement celui de la première partie, en remplaçant "périmètre" par..."aire"

Soit un rectangle de côté x et 2 cm. On construit sur deux de ses côtés consécutifs un triangle équilatéral. Lequel des trois polygones à l'aire la plus grande et pour quelle(s) valeur(s) de x?

Cette fois, la première chose que tu vas avoir à faire, c'est d'exprimer les aires de ces 3 polygônes (le rectangle et les 2 triangles) en fonction de x.

Pour répondre à ta question, tu n'as a priori pas besoin de tes équations sur les périmètres. Tu dois faire appel à tes connaissances sur les aires.

L'aire du rectangle, c'est facile : c'est .
Tu sais que l'aire d'un triangle c'est

Triangle 1 :

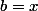
Pour la hauteur, il suffit d'appliquer Pythagore à un endroit bien précis

Donc...


Triangle 2 :




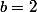
Après quoi, il faut comparer , 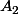et .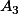

Et effectivement, cela va certainement nécessiter de résoudre une (ou plusieurs) équations du second degré.

[Effyy]

Tout d'abord merci pour ta réponse Rizmoth , c'est gentil d'avoir pris le temps... Euh par contre j'ai bien compris l'idée de Pythagore mais je comprends pas comment on fait pour tomber sur racine de 3 sur 2 en hauteur...par j'ai essayé de calculer l'aire du triangle qui fait 2 cm de côté je tombe sur racine de 3, est ce que c'est normal ou je me suis encore planté ? ^^

[Rizmoth]

Pour le triangle s'appuyant sur le côté de longueur x : le petit côté vaut x/2, l'hypoténuse, x. La hauteur h vaut alors racine (x² - (x/2)²) = racine(3x²/4) soit racine(3)*x/2.

Pour le triangle s'appuyant sur le côté de longueur 2 : eh bien c'est comme si x = 2, du coût, la hauteur vaut racine(3) * 2/2...donc racine(3) ! Tu as donc raison ;)

[Effyy]

Ah cool :) et par rapport à l'équation du second degré je vois vraiment pas du tout comment faire,pour répondre à la question j'aurais fait comme pour la première partie à l'aide du graphique et du tableur,j'ai retourné ça dans tous les sens mais j'arrive à des valeurs qui relève du paranormal 0o

[Rizmoth]

On a besoin de comparer 3 aires entre elles. Or...difficile de faire autrement que de les comparer deux à deux. Mais parmi ces 3 comparaisons, en effet, 2 d'entre elles font intervenir la résolution d'une équation du second degré.

1/ Comparer A_1 et A_2
Il suffit de calculer et d'évaluer quand cette quantité est supérieure ou inférieure à 0.

2/ Comparer A_2 et A_3


3/ Comparer A_1 et A_3