Comparaison de grands nombre avec fonction ln

[Robic]

La fonction 'devine' semble calculer la somme des termes de 1 à n, mais je ne comprends pas le rôle du 777. En fait ça a l'air de calculer 777+u(10)+u(9)+...+u(1).

Si c'est la somme des termes, ça me paraît quand même moins facile à comprendre avec la récursivité.

[takezo]

Je t'invite à modifier ton code "5*(1-((md+5)*5>reste))" par "0 if (md+5)*5>reste else 5"

Merci
C'est du Python 2.6 transposé en 3.4... Et puis, c'était un exercice de style.
Je vais essayer... Je ne sais pas tout sur Python.

C'est fait. C'est plus beau, mais sur 20000 décimales, c'est la même durée au 1/1000e près...
Demain je pousserai plus loin.

[chombier]

La fonction 'devine' semble calculer la somme des termes de 1 à n, mais je ne comprends pas le rôle du 777. En fait ça a l'air de calculer 777+u(10)+u(9)+...+u(1).

Si c'est la somme des termes, ça me paraît quand même moins facile à comprendre avec la récursivité.

C'est Ca. Moi ça me parait plus clair

si n>=1,

si n=0,

Sur un exemple aussi simple, la boucle peut paraitre plus claire. C'est sur des exemple un peu plus complexes que la récursivité donne toute sa puissance :

Dans ce sujet : http://www.maths-france.fr/Terminale/TerminaleS/ProblemesBac/AnnalesThematiques/Algorithmes/BacS_Juin2012_Obligatoire_Asie_Exo4_Enonce.pdf

En programmation récursive, ça donnerait :

Code: Tout sélectionner

def f(n, a, b)
  if n = 0 alors
    retourner (a, b)
  sinon
    retourner f(n-1, (a+b)/2, sqrt((a^2+b^2)/2)

C'est quand même plus clair que la bouillie du sujet, non ?

[chombier]

Merci
C'est du Python 2.6 transposé en 3.4... Et puis, c'était un exercice de style.
Je vais essayer... Je ne sais pas tout sur Python, moi non plus.

C'est fait. C'est plus beau, mais sur 20000 décimales, c'est la même durée au 1/1000e près...
Demain je pousserai plus loin.

Oui, il y a beaucoup de progrès avec la version 3.4 (tardifs, je dirait mais bon). Le problème est que ce n'est pas rétro compatible...

Le C de 1970 se compile encore sur le dernier GNU-C

L'opérateur ternaine ne fait rien gagner en temps d'éxécution, juste en lisibilité

Comme la récursivité (sauf qu'elle fait gagner en pouvoir d'expression aussi, surtout couplée à un langage fonctionnel) !

[Robic]

(Réaction au message de 22h15)

Ah oui c'est intéressant vu comme ça : deux suites dans la même fonction ! Mais il faut avoir l'habitude...

[paquito]

Voilà pour prouver que je plaisante pas :

Code: Tout sélectionner

#!/usr/bin/env python
# -*- coding: UTF8 -*-

from time import process_time

def rac5(prc):
    reste,md,finbcl,L=100,4,prc+1,["2"]
    for j in range(finbcl):
        md=10*md
        i=5*(1-((md+5)*5>reste))
        while (md+i)*i>> print (True+True)
2
>>>

D'autre part, quand j'écris :
i=5*(1-((md+5)*5>reste)) j'utilise bien True et False :
(md+5)*5>reste est soit True, soit False, et True et False sont automatiquement remplacés selon le cas par 1 ou 0 et le calcul effectué...
Précision : l'algorithme d'extraction de la racine carrée de 5 est basé sur la méthode de calcul à la main que j'ai apprise en classe de 4e et que bien peu de nouveaux profs connaissent...

Et voilà les 2 lignes que j'avais gardées cachées :

Code: Tout sélectionner

from sys import setrecursionlimit
setrecursionlimit(100000)

Qu'est ce qu'on est impressionné!
Déjà pour calculer , on peut utiliser
Pour initialiser à coup sur, on part de et on fait un tout petit peu de dichotomie et on arrive vite à donc .

Ensuite, , d'où , ou, . ça ira très vite sans bouffer de mémoire;
sinon, d'une part je n'ai pas apprécier ton ton de jeune branleur, et de plus,ce post n'a rien à faire dans le forum lycée. donc je n'y reviendrais plus.

[Robic]

Ce que disait Takezo est intéressant. Le ton de ses messages, c'est celui que chacun imagine puisque ce sont des messages écrits. Pour ma part j'ai lu ses messages sans rien remarquer d'inhabituel.

De plus, je ne trouve pas évident que la suite soit la plus rapide pour calculer une floppée de décimales d'une racine carrée. Certes, elle converge très vite en nombre d'itérations, mais à chaque itération il faut inverser Un, ce qui va devenir de plus en plus long à mesure qu'on aura de plus en plus de décimales. Je ne serais pas surpris que les vieilles méthodes d'extraction de racines carrées, où l'on obtient les décimales une par une (*), soient en fin de compte plus efficaces (dans ce contexte où on cherche plein de décimales, pas en général).

Enfin, la "vraie" discussion est close depuis un moment (le problème a été résolu), du coup on est comme devant la machine à café : on digresse, on papote, mais c'est intéressant je trouve.

----
(*) Un jour, par curiosité, j'en ai regardé une, il me semble qu'on obtenait les décimales de deux en deux. En tout cas c'était un peu compliqué pour moi... :marteau:

[chombier]

Ce que disait Takezo est intéressant. Le ton de ses messages, c'est celui que chacun imagine puisque ce sont des messages écrits. Pour ma part j'ai lu ses messages sans rien remarquer d'inhabituel.

De plus, je ne trouve pas évident que la suite soit la plus rapide pour calculer une floppée de décimales d'une racine carrée. Certes, elle converge très vite en nombre d'itérations, mais à chaque itération il faut inverser Un, ce qui va devenir de plus en plus long à mesure qu'on aura de plus en plus de décimales. Je m'attends plutôt à ce que les vieilles méthodes d'extraction de racines carrées, où l'on obtient les décimales une par une (*), soient en fin de compte plus efficaces (dans ce contexte où on cherche plein de décimales, pas en général).

Enfin, la "vraie" discussion est close depuis un moment (le problème a été résolu), du coup on est comme devant la machine à café : on digresse, on papote, mais c'est intéressant je trouve.

----
(*) Un jour, par curiosité, j'en ai regardé une, il me semble qu'on obtenait les décimales de deux en deux. En tout cas c'était un peu compliqué pour moi... :marteau:

+1 rien senti d'ihabituel dans les messages de Tazeko

Par contre je pense que pour calculer racine de 5, l'algo de Newton est plus rapide que la dichotomie et que la plupart des autres méthodes. La fonction est contractante et plus que ça : sa dérivée est nulle en x=racine(5)

[chombier]

je ne pensais pas que ça allait délirer autant sur le sujet (dans le bon sens bien sur) ....


j'avoue que je ne connais pas très bien tous ces nouveaux langages ... mais il semble donc que ça n'est guère mieux que si c'était plus pire ... :ptdr:

avec les progrès de ces 20 dernières années ben je trouve que c'est bien triste ... mais que signifie le mot progrès ....



pour en revenir à al récursivité ... et bien c'est beau, bref, concis ....

elle s'applique naturellement à tous les produits du modèle factorielle ... mais plus généralement à par exemple toutes les sommes où f est une fonction

puisque

et moi je veux pouvoir faire cela sans m'occuper de la pile , ou la face ou je ne sais quoi d'autre ... mais si à 1000 ça stoppe ... ben mede alors !!!!

que un coup ça me sorte peut-être un "memory overflow" parce que je pousse un peu trop ok ... j'accepte bien ...

mais donc il semble bien qu'on n'est pas fait avancé réellement le schmilblick ...(enfin j'exagère un peu)

en arrivant à la fac on était en plein dans TURBOPASCAL que je trouvais très pédagogique car très rigoureux et structuré .... avec tout de même ce défaut de déclaration de variable très lourd ...

mais si on n'a plus de déclaration de variable mais que le langage "ne reconnaît" pas true + true c'est un peu dommage ....



à Robic ::: il me semble qu'il faudrait commencer à tester la divisibilité par 2 et non par 3 pour éliminer tout nombre pair ... ?


un modeste et humble programmeur ....

:lol3:

Je reviens sur :

Pour que la pile ne t'ennuie pas, et que ca prenne autant de mémoire qu'en itératif (et avec un langage qui gère la récurât ion terminale), il faut l'ecrire autrement : en posant T(a, n, f) = a+S(n, f), et obtenir ainsi :

L'interet c'est que pour calculer T(a, n, f), il suffit de calculer T(a+f(n), n-1, f), alors que pour calculer S(n, f), il faut calculer S(f, n-1) puis ajouter f(n)

Tout est dans le "puis", c'est lui qui oblige l'interprete à empiler les appels

Plus clairement, sur un exemple, avec f(x) = x^2
S(3, f) = S(2, f) + 9 = (S(1, f) + 4) + 9 = ((S(0, f) + 1) + 4) + 9 = ((0 + 1) + 4) + 9

T(0, 3, f) = T(9, 2, f) = T(13, 1, f) = T(14, 0, f) = 14

Dans les deux cas, Python est dans les choux :
Avec S car la pile d'appel est limitée a 1000
Avec T car il ne gère par la récursivité terminale et que la pile d'appel est limitée a 1000

[takezo]

sinon, d'une part je n'ai pas apprécier ton ton de jeune branleur, et de plus,ce post n'a rien à faire dans le forum lycée. donc je n'y reviendrais plus.

Ouh là !
Je n'ai pas l'impression d'avoir manqué de respect de respect à qui que ce soit.
Désolé de t'avoir offensé, telle n'était pas mon intention : je n'ai pourtant essayé que d'utiliser un ton qui se voulait badin. C'est apparemment raté, mais j'apprécie le qualificatif de jeune, à 68 ans, ça fait plaisir. :we:

Mais je tiens à ajouter :
1. Oui mon post est hors-sujet (peut-être un peu plus que d'autres), je l'ai dit
2. Mon script n'avait pas de valeur exemplaire :
* je voulais montrer qu'il existait vraiment et qu'en Python, on pouvait bien jouer avec True et False (et accessoirement se passer de if)
* qu'effectivement, il calculait 20000 décimales.
3. En outre, le post cité montrait aussi comment outrepasser la limitation par défaut de la pile de Python à 1000 appels...

Cela dit, j'ai compris, je n'ai pas pour habitude m'incruster, je me retire sur la pointe des pieds...

[zygomatique]

merci à chombier pour son post de 23h49 ...

et une question :: dans ton deuxième code ::

il se termine par

loop(x->x^2, 5)

je ne comprends pas ce 5 ...

merci par avance ...



d'autre part tout comme robic je ne trouve pas que le toujours jeune (d'esprit :lol3: ) tazeko ait eu un ton sur lequel on ait à redire ....

il nous propose un autre exemple qui est bien connu :

le calcul de la racine carrée d'un nombre par l'algorithme (bien connu de nos ainés) utilisant l'identité remarquable

certes il est lent mais c'est un bel exercice de style pour travailler l'algorithmique et la programmation ...

il pourrait tout à fait être proposé à des élèves de terminale .... s'ils savaient que le carré d'une somme n'est pas la somme des carrés .... et s'ils savaient lire et écrire (et en particulier des calculs et qu'il existe des parenthèses) ...

et je trouve très ingénieux son calcul avec la variable booléenne ::

i=5*(1-((md+5)*5>reste))

....

ensuite c'est un problème de français et de lecture attentive pour comprendre ce calcul ... mais c'est à nouveau très riche intellectuellement : car ça implique que cette lecture doit se faire en ayant conscience de que signifient ou ce que sont les objets écrits (dans le cas présent des variables et savoir de quel type elles sont (booléenne, entière, ...)

il existe une théorie sur la vitesse de convergence d'une suite et l'algorithme de tazeko est très lent et on montre que l'algorithme est quadratique donc très rapide et permet effectivement d'avoir les décimales par 2 en gros ....

dans l'éducation ce n'est pas tant cela qui prime ... mais pour tout ce qui touche à l'informatique ça devient très important à nouveau pour obtenir en peu d'itérations très vite une bonne valeur approchée ....

on retrouve ce même problème avec toutes les théories numériques d'intégration (Runge-Kutta et autre, ...) où on arrive avec quelques modifications à accélérer la convergence ....

:lol3:

[chombier]

merci à chombier pour son post de 23h49 ...

et une question :: dans ton deuxième code ::

il se termine par

je ne comprends pas ce 5 ...

merci par avance ...

Je m'a angkor trompé

Code: Tout sélectionner

def devine2(u, n) :
  def loop(a, n) :
    si n = 0 alors
      retourner a
    sinon
      retourner loop(a+u(n), n-1)
  loop(0, n)

devine2(x->x^2, 5)

la dernière ligne appelle la fonction devine2 avec :
- comme premier argument la fonction qui à tout nombre x associe son carré
- le nombre 5

J'aurais pu l'écrire comme ceci :

Code: Tout sélectionner

def carre(x)
  retourner x * x

devine2(carre, 5)

Dans un langage fonctionnel, on peut même définir la composition de deux fonctions :

Code: Tout sélectionner

def composition(f, g)
    retourner x -> f(g(x)) ; cette procédure renvoie une autre procédure

composition(carre, x->x+1) = x->(x+1)^2
composition(x->x+1, carre) = x -> x^2+1

Avec un peu de boulot, on peut arriver à des jolies fonctions comme celle-ci, en utilisant le fait qu'une matrice est nulle si la trace du produit de cette matrice et de sa transposée est égale à zéro :

Code: Tout sélectionner

def matrice-nulle?(M) :      (* matrice-nulle? renvoie un booléen *)
  retourner trace-matrice(mul-matrice(M, transposee-matrice(M)) = 0

def egal-matrice?(A, B)
  retourner matrice-nulle?(sub-matrice(A, B))

On ne cherche pas la performance de prime abord quand on écrit ce genre de programme, mais un formalisme qui permet d'écrire des programmes qui ressemblent à la façon dont on se représente les choses objets qu'on manipule. Et qui fonctionne !

Remarquez qu'une fois de plus dans tous mes exemple il n'y a aucune affectation (pas de :=). En informatique on appelle les affectations et autres opérations qui modifient un objet en mémoire des "effets de bord", et ils sont source de beaucoup d'erreurs.

Ex scheme (mon langage préféré), cela ressemble à ça : (ceci est du *vrai* code)

Code: Tout sélectionner

(define (matrice-nulle? m)
  (= 0 (trace (mul-matrice m (transposee-matrice m)))))

(define (matrice-egal? A B)
  (matrice-nulle? (sub-matrice A B)))

[zygomatique]

bon sang de bonsoir !!! je ne vois aucune différence entre tes deux codes !!!!

en tout cas merci pour ces info ....

[paquito]

Bonjour,

C'est le côté un peu prétentieux qui m'a gêné, mais je devais être de mauvaise humeur; c'est terminé;
en ce qui concerne la méthode de Babylone, elle a l'avantage d'être valable pour tout réel A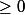 , d'être exposé au lycée et il n'y a aucun problème pendant la phase de dichotomie qui va très vite car on cherche seulement un majorant de 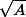tel que , ce qui permet d'avoir quel que soit A, lorsque l'on itère, la majoration Donc on peut faire une boucle pour une précision fixé pour tout A.

Par exemple, si on veut un programme qui calcule les racines carrées avec par exemples 100 000 décimales on à forcément au moins décimales exactes donc une boucle de 1 à 17
suffit et bien sûr pouvoir stocker 2 nombres avec une quantité industrielle de décimales sachant que dès que est calculé il prend la place dequi est détruit.

Ce n'est sûrement pas la meilleure méthode, mais en tout cas elle est facile à mettre en oeuvre.