Primitives

[maddanlinetant]

Bonjour,
Est ce que quelqu'un pourrait-il m'aider à calculer la primitive de cette fonction f(x) = x² + x - 3 (1 + lnx)
J'ai essayé et je trouve x (au cube) / 3 + x² / 2 - 3x

[eriadrim]

Tu as oublié d'intégrer le ln(x) ce qui fait que pour le moment tu as seulement une primitive de x² + x - 3

Après une primitive de ln est xln(x) - x (tu pourras vérifier).

Du coup avec ça tu devrais trouver ce que tu cherche ;)

[Carpate]

Une primitive de lnx est (intégration par parties) :

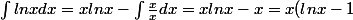[maddanlinetant]

Alors du coup ça ferait F(x) = x(au cube) / 3 + x² / 2 -3x²lnx - x

[Carpate]

Alors du coup ça ferait F(x) = x(au cube) / 3 + x² / 2 -3x²lnx - x

Plutôt :

[maddanlinetant]

Ah oui j'avais tout regroupé.. Mais alors la primitive de lnx c'est lnx - 1 ou xlnx - x ?

[laetidom]

Ah oui j'avais tout regroupé.. Mais alors la primitive de lnx c'est lnx - 1 ou xlnx - x ?

La primitive de lnx c'est xlnx - x = x(lnx-1)

[maddanlinetant]

Oui c'est ce que j'avais vu sur d'autre site alors du coup ça fait
x au cube / 3 + x² / 2 - 3x - 3x(lnx-1)

[maddanlinetant]

Ce ne serait pas plutôt : xau cube / 3 + x² / 2 - 3x - 3x (x (lnx - 1) )
?

[laetidom]

Oui c'est ce que j'avais vu sur d'autre site alors du coup ça fait
x au cube / 3 + x² / 2 - 3x - 3x(lnx-1)

sous toute réserve je trouve :

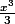
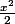
+-3xlnx

[maddanlinetant]

Comment as tu fait pour arriver au -3xlnx ?

[Buridan]

Je trouve comme Carpate:

[maddanlinetant]

Mh Carpate n'a pas trouvé la même chose que toi non ?

[Buridan]

Mh Carpate n'a pas trouvé la même chose que toi non ?

Si, si... Développe sa parenthèse et la mienne et tu trouveras la même chose... :lol3:

[maddanlinetant]

Oh oui exact, pardon :)
Donc ce doit être ça, je n'ai pas bien compris le -3x -3x (lnx-1)

[laetidom]

Oh oui exact, pardon
Donc ce doit être ça, je n'ai pas bien compris le -3x -3x (lnx-1)

excuse-moi j'étais parti,

fonction :
x²+x-3(1+lnx)=x²+x-3-3lnx__________(en développant)

primitive :
(x^3/3) +(x²/2)-3x-3(xlnx-x)

(x^3/3) +(x²/2)-3x-3xlnx+3x

(x^3/3) +(x²/2)-3xlnx________car-3x+3x=0

[maddanlinetant]

Aaah oui d'accord j'ai compris, merci beaucoup :D

[laetidom]

Aaah oui d'accord j'ai compris, merci beaucoup

A ton service ! @+