Salut,
Posons
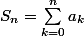
et
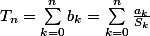
.
Les suites
_{n\geq0})
et
_{n\geq0})
sont croissantes donc convergentes ssi elles sont majorées.


donc
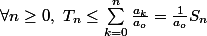
:
Si
_{n\geq0})
est majorée (par

), alors
_{n\geq0})
est majorée (par

).

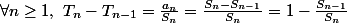
donc
}\)
d'où (récurrence)
}\)
et
=\ln(S_o)-\sum_{k=1}^n\ln\big(1-(T_k-T_{k-1})\big))
.
(noter que
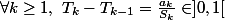
)
Si
_{n\geq0})
convergente vers

, alors
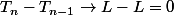
lorsque
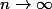
donc il existe

tel que

d'où (T.A.F.)
\big)\leq 2(T_k-T_{k-1}))
et donc
\leq \ln(S_o)-\sum_{k=1}^{n_o}\ln\big(1-(T_k-T_{k-1})\big)+2\sum_{k=n_o+1}^{n}(T_k-T_{k-1}))
.
Or
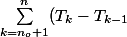=T_n-T_{n_o}\leq L-T_{n_o})
donc la suite
)_{n\geq 0})
est bornée donc la suite
_{n\geq 0})
aussi.
Remarque : En prenant
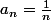
voire
})
, on peut voir que dans ces cas où la série
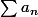
diverge, la série
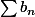
diverge aussi, mais beaucoup moins vite, plus précisément,
)
.
Cela explique la relative complexité de la partie "
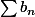
C.V.

C.V." qui équivaut évidement à "
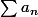
D.V.

D.V."
Il y a sans doute plus simple, mais a mon avis, il faut forcément comparer
)
avec

...