Exercice Dérivée

[aurore508]

Bonjour,
je suis actuellement en 1èreS et mon professeur nous a donné comme exercice :

Quel doit être le format (hauteur, rayon) d’une boite de conserve cylindrique pour que, pour un volume donné, la quantité de métal pour la concevoir, qu’on supposera proportionnelle à sa surface, soit minimale.

Je sais que le volume d'un cylindre est : pi*r²*h
Mais n'ayant aucune autre donnée, je ne sais pas comment faire.
Il y a t il quelqu'un qui puisse m'aider ?
Cordialement

[chan79]

salut
Exprime la hauteur en fonction de R (le volume est constant)
Puis, exprime la surface en fonction de R.

[aurore508]

salut
Exprime la hauteur en fonction de R (le volume est constant)
Puis, exprime la surface en fonction de R.

Pourrez- tu donner plus d'explications s'il te plait ?

[aurore508]

salut
Exprime la hauteur en fonction de R (le volume est constant)
Puis, exprime la surface en fonction de R.

Comment exprimer h par rapport à r ?

[chan79]

Comment exprimer h par rapport à r ?

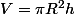
Exprime l'aire en fonction de R (V est fixé)

[aurore508]

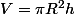
Exprime l'aire en fonction de R (V est fixé)

On trouve : Aire = 2piRh où h= V/(pir²)
A = 2r*V/r²
A = 2*V/r

C'est ça ? Mais après ?

[chan79]

On trouve : Aire = 2piRh où h= V/(pir²)
A = 2r*V/r²
A = 2*V/r

C'est ça ? Mais après ?

Il faut sans doute tenir compte du fond et du couvercle

[aurore508]

Il faut sans doute tenir compte du fond et du couvercle

Désolé de te déranger mais je ne comprends pas du tout..

[chan79]

Désolé de te déranger mais je ne comprends pas du tout..

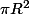
Une boîte de conserve a bien un fond et un couvercle d'aire chacun , à ajouter à l'aire latérale.

[aurore508]

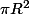
Une boîte de conserve a bien un fond et un couvercle d'aire chacun , à ajouter à l'aire latérale.

D'accord, donc j'ai trouvé ça : (V/piR²)+2pi+2r²

[chan79]

D'accord, donc j'ai trouvé ça : (V/piR²)+2pi+2r²

non
c'est

Etudie cette fonction de variable R

[aurore508]

non
c'est

Etudie cette fonction de variable R

Et donc cette équation c'est quoi exactement ? La surface ?
Pourquoi est-ce 2V/R ?

Merci beaucoup déjà

[aurore508]

non
c'est

Etudie cette fonction de variable R

Et comment étudier cette fonction ? Avec une dérivée ? Je comprends rien

[chan79]

Et comment étudier cette fonction ? Avec une dérivée ? Je comprends rien

ton post est intitulé Exercice Dérivée
si on remplace R par x, il s'agit d'étudier les variations de f telle que

[aurore508]

ton post est intitulé Exercice Dérivée
si on remplace R par x, il s'agit d'étudier les variations de f telle que

D'accord, mais V pose problème non ? On en fait quoi du V?

[chan79]

D'accord, mais V pose problème non ? On en fait quoi du V?

C'est une constante.
La valeur de R dépend de V.

[aurore508]

C'est une constante.
La valeur de R dépend de V.

Oui mais comment étudier la fonction sans connaitre la valeur de V ?

[paquito]

Comme te l'a montré chan, A(r)=2pir²+2V/r, où r est la variable et V une constante; d'où

A'(r)=4pir-2V/r²>0 pour 4pir>2V/r²<=> r^3>V/2pi<=>r>(V/2pi)^(1/3) car tout est>0 et la fonction
x->x^3 est strictement croissante (x^(1/3)) correspond à la racine cubique de x)

[aurore508]

Comme te l'a montré chan, A(r)=2pir²+2V/r, où r est la variable et V une constante; d'où

A'(r)=4pir-2V/r²>0 pour 4pir>2V/r² r^3>V/2pir>(V/2pi)^(1/3) car tout est>0 et la fonction
x->x^3 est strictement croissante (x^(1/3)) correspond à la racine cubique de x)

Donc x doit être égale à combien?

[aurore508]

Comme te l'a montré chan, A(r)=2pir²+2V/r, où r est la variable et V une constante; d'où

A'(r)=4pir-2V/r²>0 pour 4pir>2V/r² r^3>V/2pir>(V/2pi)^(1/3) car tout est>0 et la fonction
x->x^3 est strictement croissante (x^(1/3)) correspond à la racine cubique de x)

Donc x doit être égale à combien?