Polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 14 Mar 2014, 14:44
par Raphoul » 14 Mar 2014, 14:44
Bonjour,
je dois chercher, en remarquant que 16 est une puissance de 2, les racines du polynôme
=X^4+16)
Donner alors une factorisation dans C[X] et R[X] de P(X) en produit de polynôme irréductibles.
Donc j'écris
=X^4+2^4)
mais après je ne sais pas comment faire
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 14 Mar 2014, 14:59
par jlb » 14 Mar 2014, 14:59
Salut, essaie d'abord X^4-(4i)², que tu peux factoriser facilement ensuite sur C
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 14 Mar 2014, 15:01
par wserdx » 14 Mar 2014, 15:01
Ben, on appelle racine d'un polynôme P, les solutions de l'équation P(x)=0.
Donc ici on écrit l'équation en remplaçant P par sa valeur et on résout sur

de préférence en mettant l'équation sous la forme

.
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 14 Mar 2014, 15:11
par Raphoul » 14 Mar 2014, 15:11
je ne vois pas trop comment partir
je sais qu'il faut que je résolve P(x)=0
je remplace P(x) par sa valeur mais je ne vois pas après
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 14 Mar 2014, 15:20
par wserdx » 14 Mar 2014, 15:20
Je t'ai proposé d'écrire -16 en forme polaire, c'est à dire trouver

et

tels que

. Sais-tu le faire?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 14 Mar 2014, 15:21
par Carpate » 14 Mar 2014, 15:21
Raphoul a écrit:je ne vois pas trop comment partir
je sais qu'il faut que je résolve P(x)=0
je remplace P(x) par sa valeur mais je ne vois pas après
)
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 14 Mar 2014, 18:11
par Raphoul » 14 Mar 2014, 18:11
wserdx a écrit:Je t'ai proposé d'écrire -16 en forme polaire, c'est à dire trouver

et

tels que

. Sais-tu le faire?
oui ça fais


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 14 Mar 2014, 19:22
par chan79 » 14 Mar 2014, 19:22
Raphoul a écrit:oui ça fais

Salut

si
^4=-1)
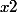
est une racine quatrième de -1
les racines quatrièmes de -1 sont
})
pour k prenant les valeurs 0, 1, 2 et 3

-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 15 Mar 2014, 07:20
par fibonacci » 15 Mar 2014, 07:20
Bonjour;
^2 - 8x^2 \\ <br /> \\ <br /> (x^2 + 4)^2 - 8x^2 = \left( {(x^2 + 4) - 2\sqrt 2 x} \right)\left( {(x^2 + 4) + 2\sqrt 2 x} \right) \\ <br /> = (x^2 - 2\sqrt 2 x + 4)(x^2 + 2\sqrt 2 x + 4) = AB \\ <br /> \\ \\<br /><br /> x_{1,2} = - \frac{{ - 2\sqrt 2 \pm \sqrt {( - 2\sqrt 2 )^2 - 4(4)} }}{2} = - \frac{{ - 2\sqrt 2 \pm 2i\sqrt 2 }}{2} = \sqrt 2 (1 \mp i) \\ <br /> \end{array})
... etc
-
Black Jack
 par Black Jack » 15 Mar 2014, 10:04
par Black Jack » 15 Mar 2014, 10:04
x^4 + 16 = 0
(x²)² - (4i)² = 0
(x² - 4i).(x² + 4i) = 0
a)
x² = 4i = 4.e^(Pi/2 + 2k.Pi)
x = 2.e^(Pi/4 + k.Pi)
x1 = 2.e^(Pi/4) = 2.(cos(Pi/4) + i.sin(Pi/4)) = V2 + i.V2
x2 = 2.e^(Pi/4 + Pi) = -V2 - i.V2
b)
x² = -4i = 4.e^(-Pi/2 + 2k.Pi)
x = 2.e^(-Pi/4 + k.Pi)
x3 = 2.e^(-Pi/4) = 2.(cos(-Pi/4) + i.sin(-Pi/4)) = V2 - i.V2
x4 = 2.e^(-Pi/4 + Pi) = -V2 + i.V2
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités