Primitives
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 20 Fév 2014, 20:34
par wakaloup35 » 20 Fév 2014, 20:34
Salut,
J'arrive pas à le commencer cet exo :
On se propose de déterminer une valeur approchée, à
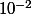
près, l'intégrale
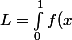 dx)
où f est la fonction définie sur [0;1] par
=\frac{e^{-x}}{2-x})
.
1- Démontrer que pour tout x de [0;1],
 \le \frac{1}{2})
Voilà, il y a d'autres question mais je me débrouillerai, j'arrive juste pas à commencer.
merci de votre aide
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 20 Fév 2014, 20:53
par Carpate » 20 Fév 2014, 20:53
As-tu étudié les variations de f(x) sur [0;1] ? (calcul de la dérivée, etc)
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 20 Fév 2014, 21:09
par wakaloup35 » 20 Fév 2014, 21:09
f est décroissante sur [0;1]
-
landagama
- Membre Relatif
- Messages: 228
- Enregistré le: 03 Sep 2013, 11:32
-
 par landagama » 20 Fév 2014, 22:05
par landagama » 20 Fév 2014, 22:05
Comme f est décroissante sur [0;1], alors, pour
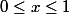
, on a
\geq f(x) \geq f(1))
.
Tu calcules f(0) ef f(1) et c'est terminé !
J'espère que tu y arriveras !
Si ça te dit de visiter mon blog de maths : http://www.bossetesmaths.com
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 20 Fév 2014, 22:10
par wakaloup35 » 20 Fév 2014, 22:10
ah en fait il suffit de commencer par
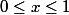
et ne pas oublier à la fin que

merci ^^
-
wakaloup35
- Membre Relatif
- Messages: 137
- Enregistré le: 01 Nov 2011, 16:34
-
 par wakaloup35 » 20 Fév 2014, 22:27
par wakaloup35 » 20 Fév 2014, 22:27
je bloque sur la question 2 aussi en fait :
J et K sont les intégrales tels que :
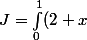e^{-x} dx)
et
 dx)
a) Prouvez que

b) Utilisez l'encadrement du 1- pour démontrer que

c) Démontrez que J+K=4L
d) En déduire un encadrement de L puis une valeur approchée de L à
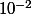
près.
J'ai l'impression qu'il y a un lien entre f(x) et
e^{-x})
mais que faire ?
-
parkstreet
- Messages: 6
- Enregistré le: 01 Mar 2014, 19:29
-
 par parkstreet » 01 Mar 2014, 19:40
par parkstreet » 01 Mar 2014, 19:40
Bonjour à tous.
D'après l'encadrement précédent, tu peux obtenir une inégalité sur l'intégrale K :

Comme
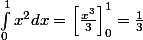
, on a :

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
près, l'intégrale
où f est la fonction définie sur [0;1] par
.
