Equations à "résultats limités"

[HexaCoder]

Salut !

En travaillant sur un projet de cryptographie je me suis posé la question suivante :

Peut on créer une équation f (x) où x appartient à l'interval [0; +infinie] et oú le resultat
ne puisse être compris que dans l'interval par exemple [0; 65] ?

Alors possible ou non ?

++

[nodjim]

Bien sûr. Par exemple, tu écrits les nombres modulo 66. Mais ce ne sera pas une bijection, et ça n'aura pas beaucoup d'intérêt en crypto.
Connais tu la crypto vigénère ?

[HexaCoder]

Merci de cette reponse si rapide mais si je fais un modulo le resultat poura appartenir à D ?
Oui bien sûr je connais la crypto vigenère ! En faite c'est un projet de crypto informatique :
et je me sert des maths pour le" transfert" d'une lettre vers une autre un peut comme en
Base64

[perM11]

Bien sur que c'est possible, il suffit de prendre une fonction de R+ avec f(0)=0 et lim fini non nulle en +inf et continue strictement croissante, ensuite tu multiplie par 65 si ta limite est 1 et tu auras même une bijection

[Vupen]

Ou bien,

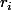
avec les des nombres appartenant à [0, 65] et un entier naturel quelconque.

Tu obtiens donc un polynome après développement et les solutions de (si j'ai bien compris ton problème) sont tous dans l'intervalle [0, 65].

[kapersky]

la fonction f(x)=(65x):(x+1) verifie ta condition

[Robic]

Ou bien :
g(x) = (130/pi) Arctan(x)
h(x) = 65 (1-exp(-x))
k(x) = 65 cos( Arctan(x) )
l(x) = 65 exp(-x²/2)
m(x) = 65 / (x²+1)
n(x) = 65 ( exp(x) - 1) / exp(x)
etc.