Suites et integrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
par Haki » 26 Mar 2012, 17:42
Bonjour, pouvez vous m'aider ?
(Un) est la suite définie par :
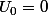
et pour tout entier n,
1) Calculez
et
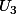
j'ai un probleme car je tombe sur racine de racine de racine ...
2) Prouvez que la suite (Un) est croissante et majorée par 3. Que pouvez vous en déduire?
je ne sais pas comment connaitre le signe de
ni comment prouver qu'elle est majorée par 3...
3) Quelle est la limite de (Un) ? Justifiez votre reponse.
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
par titine » 26 Mar 2012, 17:51
j'ai un probleme car je tombe sur racine de racine de racine ...
Ce n'est pas un problème !
As tu vu les démonstrations par récurrence ?
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
par Haki » 26 Mar 2012, 17:53
titine a écrit:Ce n'est pas un problème !
As tu vu les démonstrations par récurrence ?
oui je les ai vues
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 26 Mar 2012, 17:55
Haki a écrit:Bonjour, pouvez vous m'aider ?
(Un) est la suite définie par :
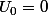
et pour tout entier n,
1) Calculez
et
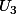
j'ai un probleme car je tombe sur racine de racine de racine ...
2) Prouvez que la suite (Un) est croissante et majorée par 3. Que pouvez vous en déduire?
je ne sais pas comment connaitre le signe de
ni comment prouver qu'elle est majorée par 3...
3) Quelle est la limite de (Un) ? Justifiez votre reponse.
bonsoir
tu peux montrer facilement par récurrence que Un<=3
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
par Haki » 26 Mar 2012, 17:55
je viens de voir comment montrer qu'elle est majorée mais je ne sais pas quoi faire pour le sens de variation
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 26 Mar 2012, 18:00
Haki a écrit:je viens de voir comment montrer qu'elle est majorée mais je ne sais pas quoi faire pour le sens de variation
transforme Un+1 - Un en multipliant en haut et en bas par sa quantité conjuguée
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
par Haki » 26 Mar 2012, 18:01
c'est effectivement ce que j'ai fait mais je ne sais pas etudier le signe du denominateur
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 26 Mar 2012, 18:09
Haki a écrit:c'est effectivement ce que j'ai fait mais je ne sais pas etudier le signe du denominateur
Un est toujours positif
la somme de 2 positifs est positive
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
