Suites et integrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 18:13
par Haki » 23 Mar 2012, 18:13
Bonjour,
On a
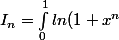 dx)
Il faut
etudier les varations de cette suite.
Je sais qu'il faut faire
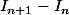
mais je n'arrive pas a aboutir a un resultat en calculant.
on trouve qu'elle est croissante et d'après les questions précedentes on en déduit qu'elle est convergente.
Ensuite j'étudie les variations de
=ln(1+x)-x)
sur

je dois en
deduire que  \le x^n)
je ne sais pas comment faire..
Et enfin je dois
trouver la limite de la suite )
MERCI d'avance !
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 23 Mar 2012, 18:32
par Manny06 » 23 Mar 2012, 18:32
Haki a écrit:Bonjour,
On a
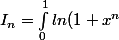 dx)
Il faut
etudier les varations de cette suite.
Je sais qu'il faut faire
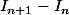
mais je n'arrive pas a aboutir a un resultat en calculant.
on trouve qu'elle est croissante et d'après les questions précedentes on en déduit qu'elle est convergente.
Ensuite j'étudie les variations de
=ln(1+x)-x)
sur

je dois en
deduire que  \le x^n)
je ne sais pas comment faire..
Et enfin je dois
trouver la limite de la suite )
MERCI d'avance !
sur [0;1] compare x^n et x^(n+1)
tu en deduiras facilement la monotonie de In (mais je pense qu'elle est décroissante et minorée)
si tu as étudié les variations de g tu as du trouver qu'elle était decroissante à partir de 0 donc négative
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 18:41
par Haki » 23 Mar 2012, 18:41
Manny06 a écrit:sur [0;1] compare x^n et x^(n+1)
tu en deduiras facilement la monotonie de In (mais je pense qu'elle est décroissante et minorée)
si tu as étudié les variations de g tu as du trouver qu'elle était decroissante à partir de 0 donc négative
Je crois que j'ai trouvé a condition que x^n.x^n = x^(n+1)
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 23 Mar 2012, 18:51
par Manny06 » 23 Mar 2012, 18:51
Haki a écrit:Je crois que j'ai trouvé a condition que x^n.x^n = x^(n+1)
NON
x^(n+1)=(x^n)*x
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 18:53
par Haki » 23 Mar 2012, 18:53
Manny06 a écrit:NON
x^(n+1)=(x^n)*x
effectivement, je viens de comprendre mon erreur, merci! Pouvez vous m'aider pour la suite ?
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 23 Mar 2012, 19:13
par Manny06 » 23 Mar 2012, 19:13
Haki a écrit:effectivement, je viens de comprendre mon erreur, merci! Pouvez vous m'aider pour la suite ?
je t'ai déjà donné des indications
à quel endroit bloques-tu ?
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 19:14
par Haki » 23 Mar 2012, 19:14
Manny06 a écrit:je t'ai déjà donné des indications
à quel endroit bloques-tu ?
Pardon je me suis mal exprimée. J'ai pu trouvée qu'elle etait decroissante grace a votre indication. Je voulais savoir si vous pouviez maintenant m'aider avec les 2 autres questions ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 20:09
par Judoboy » 23 Mar 2012, 20:09
Pour la 2, tu as ln(1+x) < x quelque soit x>0, c'est vrai en particulier pour x^n.
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 20:21
par Haki » 23 Mar 2012, 20:21
Judoboy a écrit:Pour la 2, tu as ln(1+x) 0, c'est vrai en particulier pour x^n.
comment expliquer que c'est vrai pour x^n ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 20:31
par Judoboy » 23 Mar 2012, 20:31
ln(1+y) < y est vrai quelque soit y > 0, et quelque soit y > 0 il existe x > 0 tel que y = x^n.
Tu as donc ln(1+x^n) < x^n.
Pour la 3 tu encadres In.
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 20:33
par Haki » 23 Mar 2012, 20:33
Judoboy a écrit:ln(1+y) 0, et quelque soit y > 0 il existe x > 0 tel que y = x^n.
Tu as donc ln(1+x^n) < x^n.
Pour la 3 tu encadres In.
d'accord merci beaucoup! et pour la limite de x^n je peux dire que c'est + l'infini en +l'infini directement ?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 20:37
par Judoboy » 23 Mar 2012, 20:37
Haki a écrit:d'accord merci beaucoup! et pour la limite de x^n je peux dire que c'est + l'infini en +l'infini directement ?
Oulah non, x varie entre 0 et 1, il va plutôt se passer l'inverse.
Calcule l'intégrale de 0 à 1 de x^n, et sers-toi des propriétés que tu connais sur les intégrales.
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 20:40
par Haki » 23 Mar 2012, 20:40
Judoboy a écrit:Oulah non, x varie entre 0 et 1, il va plutôt se passer l'inverse.
Calcule l'intégrale de 0 à 1 de x^n, et sers-toi des propriétés que tu connais sur les intégrales.
Si je ne me suis pas trompée la limite de

est 0 non?
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 20:41
par Judoboy » 23 Mar 2012, 20:41
Haki a écrit:Si je ne me suis pas trompée la limite de

est 0 non?
Oui, parce que ?
-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 21:23
par Haki » 23 Mar 2012, 21:23
Judoboy a écrit:Oui, parce que ?
l'integrale de x^n donne 1/(n+1) qui tend vers 0 et In est superieure a 0 donc d'après le theoreme des gendarmes..
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 23 Mar 2012, 21:43
par Judoboy » 23 Mar 2012, 21:43
Haki a écrit:l'integrale de x^n donne 1/(n+1) qui tend vers 0 et In est superieure a 0 donc d'après le theoreme des gendarmes..
Bon bah je crois que c'est fini

-
Haki
- Membre Relatif
- Messages: 114
- Enregistré le: 10 Nov 2011, 20:53
-
 par Haki » 23 Mar 2012, 22:20
par Haki » 23 Mar 2012, 22:20
Judoboy a écrit:Bon bah je crois que c'est fini

merci beaucoup vraiment!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
