bonjour à tous .j ai des exo à faire sur les primitives mais j'ai quelques petites interrogations.les voici:
f(x)=2x(1+x^2)^7
F(x)=x^2* ((1+x^2)^8)/8 ---------- resultat ((1+x^2)^8)/8
ou est passé mon 2x
f(x)=1/(3x-1)^2
F(x)=-1/(3x-1)-------reponse -1/3(3x-1)
d'ou sort le 3 au denominateur??
voila si quelqu'un pourrait me renseigner
merci d avance.
Primitives
11 messages
- Page 1 sur 1
par fonfon » 15 Mar 2007, 18:26
salut,
en fait tu remarques que ta fonction est de la forme u'(x)*u^n(x) donc une primitive est
en effet
=2x(1+x^2)^7)
idée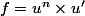
=> 
on pose u(x)=1+x² donc u'(x)=2x
tu voies bien que
=2x\times(1+x^2)^7=u'(x)\times{u^n(x)})
avec n=7
donc une primitive est
=\frac{u^{n+1}}{n+1}+k)
=\frac{u^8}{8}+k)
=\frac{(1+x^2)^8}{8}+k)
je repasses apres pour 'autre il faut que j'aille bouger ma voiture
bonjour à tous .j ai des exo à faire sur les primitives mais j'ai quelques petites interrogations.les voici:
f(x)=2x(1+x^2)^7
F(x)=x^2* ((1+x^2)^8)/8 ---------- resultat ((1+x^2)^8
en fait tu remarques que ta fonction est de la forme u'(x)*u^n(x) donc une primitive est
en effet
idée
on pose u(x)=1+x² donc u'(x)=2x
tu voies bien que
donc une primitive est
je repasses apres pour 'autre il faut que j'aille bouger ma voiture
par bastien83 » 15 Mar 2007, 19:30
comme qui dirait bien vu l'aveugle.
j'avais pas remarqué que f(x) etait de cette forme.Je comprend mieux maintenant.
j'avais pas remarqué que f(x) etait de cette forme.Je comprend mieux maintenant.
par bastien83 » 15 Mar 2007, 19:53
si je peux abuser de votre aide,j'ai une autre petite question:
f(x)=(4x^2)/(x^3+8)^3
je ne trouve pas la forme de f(x) afin d en deduire la primitive.
f(x)=(4x^2)/(x^3+8)^3
je ne trouve pas la forme de f(x) afin d en deduire la primitive.
par fonfon » 15 Mar 2007, 19:54
pour l'autre tu peux ecrire que
^2}=(3x-2)^{-2})
idée f=u'(x)*u(x)^n =>
on pose u(x)=3x-2 donc u'(x)=3
dans=(3x-1)^{-2})
on a pas tout à fait u'(x)*u^n(x) donc il faut enlever ce qui est en trop
donc
=3\times(3x-1)^{-2}\times\frac{1}{3})
=\frac{1}{3}\times{u'(x)}\times{u^{-2}(x)})
donc
=\frac{1}{3}\frac{u^{-2+1}}{-2+1}+k)
=\frac{1}{3}\frac{(3x-1)^{-1}}{-1}+k)
=-\frac{1}{3(3x-1)}+k)
idée f=u'(x)*u(x)^n =>
on pose u(x)=3x-2 donc u'(x)=3
dans
donc
donc
par fonfon » 15 Mar 2007, 19:57
si je peux abuser de votre aide,j'ai une autre petite question:
f(x)=(4x^2)/(x^3+8)^3
je ne trouve pas la forme de f(x) afin d en deduire la primitive.
il faut ecrire que
et là c'est encore de la forme u(x)*u^n(x) à quelque chose près
par bastien83 » 17 Mar 2007, 08:39
merci de votre aide.Mais j ai un autre ptt probleme.
on me demande de trouver la primitive de 1/(x-4) sur l interval ]4;+inf[.
la pas de probleme.
mais apres on me demande de trouver la primitive de la meme fonction mais sur l interval ]-inf;4[ et la c'est le drame par ma primitive (ln(x) n'est pas def sur ce I)
comme puis je faire??
on me demande de trouver la primitive de 1/(x-4) sur l interval ]4;+inf[.
la pas de probleme.
mais apres on me demande de trouver la primitive de la meme fonction mais sur l interval ]-inf;4[ et la c'est le drame par ma primitive (ln(x) n'est pas def sur ce I)
comme puis je faire??
par fonfon » 17 Mar 2007, 08:58
salut,
rappel:
Sur tout intevalle I où u ne s'anule pas, une primitive de
est 
.Il peut-être donc necessaire ensuite d'expliciter la primitive seln les intervalles
rappel:
Sur tout intevalle I où u ne s'anule pas, une primitive de
par bastien83 » 17 Mar 2007, 10:01
c'est ce que j ai fais pour le premier interval.Je trouve que F(x)=ln(x-4)+k
mais cette primitive n'est pas bonne sur ]-inf;4[.
mais cette primitive n'est pas bonne sur ]-inf;4[.
par fonfon » 17 Mar 2007, 10:06
il faut que tu connaisses le signe de x-4 sur ]-inf,4[
pour x dans ]-inf,-4[ x-4<0 donc |x-4|=-x+4
donc sur ]-inf,4[ une primitive de 1/(x-4) est ln(-x+4)+k
pour x dans ]-inf,-4[ x-4<0 donc |x-4|=-x+4
donc sur ]-inf,4[ une primitive de 1/(x-4) est ln(-x+4)+k
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 224 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :