Primitives
23 messages
- Page 1 sur 2 - 1, 2
Primitives
Bonjour, j'ai un exercice à faire sur les primitives. Il faut déterminer une primitive pour chaque fonction. J'ai essayé de le faire mais je doute de mes réponses.
f1 : 3x^2 + 4x / x^3 + 2x^2 -5 sur 2; + l'infini . La primitive que j'ai trouvé : ln(x^3 + 2x^2 -5)
f2 : -10x / (5x^2 + 7) ^2 sur R. La primitive que j'ai trouvé : -5x^2 / 10/3 x^3 + 14x
f3 : - e^ 1/x / x^2 sur 0 ; + l'infini. Par contre celle la je ne sais pas comment faire.
f4 : xe^x^2-5 sur I = R. La primitive que j'ai trouvé : 1/2 e^x^2
f5 : 1 / x ln(x) avec I = 0; + l'infini. J'hésite entre 1/x / ln(x) ou ln( ln (x))
f6 : 4x^3 -6x / x^4 - 3x^2 + 5 sur R. La primitive que j'ai trouvé : 3/4x^4 -3x^2 / 1-5x^5 - x^3 = 5x
f7 : e racine carré de x / 2 racine carré de x sur 0 ; + l'infini. Je ne sais pas comment faire non plus.
f8 : -2 -5 / x^4 +10 x^3 +25 x^2 sur 0 + l'infini. La primitive que j'ai trouvé : -x^2 -5 / 1/5x^5+2.5x^4+12.5 x^3
J'ai du mal avec ce chapitre et j'espère vraiment que quelqu'un pourra m'aider.
f1 : 3x^2 + 4x / x^3 + 2x^2 -5 sur 2; + l'infini . La primitive que j'ai trouvé : ln(x^3 + 2x^2 -5)
f2 : -10x / (5x^2 + 7) ^2 sur R. La primitive que j'ai trouvé : -5x^2 / 10/3 x^3 + 14x
f3 : - e^ 1/x / x^2 sur 0 ; + l'infini. Par contre celle la je ne sais pas comment faire.
f4 : xe^x^2-5 sur I = R. La primitive que j'ai trouvé : 1/2 e^x^2
f5 : 1 / x ln(x) avec I = 0; + l'infini. J'hésite entre 1/x / ln(x) ou ln( ln (x))
f6 : 4x^3 -6x / x^4 - 3x^2 + 5 sur R. La primitive que j'ai trouvé : 3/4x^4 -3x^2 / 1-5x^5 - x^3 = 5x
f7 : e racine carré de x / 2 racine carré de x sur 0 ; + l'infini. Je ne sais pas comment faire non plus.
f8 : -2 -5 / x^4 +10 x^3 +25 x^2 sur 0 + l'infini. La primitive que j'ai trouvé : -x^2 -5 / 1/5x^5+2.5x^4+12.5 x^3
J'ai du mal avec ce chapitre et j'espère vraiment que quelqu'un pourra m'aider.
Re: Primitives
f1 du type u'/u => une primitive est ln|u|
f2 du type -u'/u² => une primitive est 1/u
f3 du type u' e^u => une primitive est e^u
f4 du type u' e^u/2 + K => une primitive est e^u/2 + Kx
f5 du type u'u (si c'est bien ln(x)/x) => une primitive est u²/2
f6 idem f1
f7 idem f3
f8 tu peux réécrire plus lisiblement ?
f2 du type -u'/u² => une primitive est 1/u
f3 du type u' e^u => une primitive est e^u
f4 du type u' e^u/2 + K => une primitive est e^u/2 + Kx
f5 du type u'u (si c'est bien ln(x)/x) => une primitive est u²/2
f6 idem f1
f7 idem f3
f8 tu peux réécrire plus lisiblement ?
Re: Primitives
Merci pour l'aide!
J'ai refait certains calculs :
f1 : je pense que c'était correct?
f2 : d'après mon nouveau calcul une primitive est : 1/-5x ?
f3 et f7 : je n'ai pas compris parce que c'est une division et la formule est une multiplication
f4 : je crois que c'était bon au début
f5 : ce n'est pas ln(x) / x mais 1 / x ln(x)
f6 : j'ai trouvé ln(x^4 - 3x^2 + 5 )
f8 : la fonction est : -2x -5 divisé par x^4 + 10x^3 + 25x^2
J'ai refait certains calculs :
f1 : je pense que c'était correct?
f2 : d'après mon nouveau calcul une primitive est : 1/-5x ?
f3 et f7 : je n'ai pas compris parce que c'est une division et la formule est une multiplication
f4 : je crois que c'était bon au début
f5 : ce n'est pas ln(x) / x mais 1 / x ln(x)
f6 : j'ai trouvé ln(x^4 - 3x^2 + 5 )
f8 : la fonction est : -2x -5 divisé par x^4 + 10x^3 + 25x^2
Re: Primitives
Oui à condition de vérifier quebrets a écrit:f1 : je pense que c'était correct?
Nonbrets a écrit:f2 : d'après mon nouveau calcul une primitive est : 1/-5x ?
f2 du type -u'/u²
Que vaut u ?
brets a écrit:f3 et f7 : je n'ai pas compris parce que c'est une division et la formule est une multiplication
Que vaut u ?
Que vaut u ?
Tu as oublié le -5brets a écrit:f4 : je crois que c'était bon au début
Alors il faut écrire 1 / (x ln(x))brets a écrit:f5 : ce n'est pas ln(x) / x mais 1 / x ln(x)
Que vaut u ?
Oui mais il faut vérifier quebrets a écrit:f6 : j'ai trouvé ln(x^4 - 3x^2 + 5 )
brets a écrit:f8 : la fonction est : -2x -5 divisé par x^4 + 10x^3 + 25x^2
OK donc ça fait
Re: Primitives
Merci beaucoup ça m'aide vraiment!
f1 : j'ai trouvé 0.41 donc c'est faux mais je pense que c'est à cause du x^3
f2 : u vaut 5x^2 donc la primitive est : 1 / 5x^2 + 7 ?
f3 : u vaut 1/x donc la primitive est : e^1/x? Il faut quand même vérifier que c'est supérieur à 0 alors que c'est e^x?
f7 : u = racine carré de x donc F(x) = e ^racine carré de x
f4 : F(x) = 1/2 e^x+5 ?
f5 : F(x) = ln (ln(x)) ? Il faut également vérifier que ce soit plus grand que 1?
f6 : j'ai trouvé un nombre négatif donc mon calcul est faux mais je ne sais pas comment faire autrement...
f8 : u = x^2 + 5x donc F(x) = 1/x^2+5x ?
Merci encore..
f1 : j'ai trouvé 0.41 donc c'est faux mais je pense que c'est à cause du x^3
f2 : u vaut 5x^2 donc la primitive est : 1 / 5x^2 + 7 ?
f3 : u vaut 1/x donc la primitive est : e^1/x? Il faut quand même vérifier que c'est supérieur à 0 alors que c'est e^x?
f7 : u = racine carré de x donc F(x) = e ^racine carré de x
f4 : F(x) = 1/2 e^x+5 ?
f5 : F(x) = ln (ln(x)) ? Il faut également vérifier que ce soit plus grand que 1?
f6 : j'ai trouvé un nombre négatif donc mon calcul est faux mais je ne sais pas comment faire autrement...
f8 : u = x^2 + 5x donc F(x) = 1/x^2+5x ?
Merci encore..
Re: Primitives
Il faut que tu m'expliques comment tu arrives à ca ??brets a écrit:f1 : j'ai trouvé 0.41
Oui sauf que c'est UNE primitive et qu'il faut mettre des parenthèses 1/(5x^2 + 7)brets a écrit:f2 : u vaut 5x^2 donc la primitive est : 1 / 5x^2 + 7 ?
Ouibrets a écrit:f3 : u vaut 1/x donc la primitive est : e^1/x?
??brets a écrit:Il faut quand même vérifier que c'est supérieur à 0 alors que c'est e^x?
Ouibrets a écrit:f7 : u = racine carré de x donc F(x) = e ^racine carré de x
Pourquoi +5 ? Il faut intégrer -5brets a écrit:f4 : F(x) = 1/2 e^x+5 ?
u'/u s'intègre en ln|u|brets a écrit:f5 : F(x) = ln (ln(x)) ? Il faut également vérifier que ce soit plus grand que 1?
Comment as-tu fait ?brets a écrit:f6 : j'ai trouvé un nombre négatif donc mon calcul est faux mais je ne sais pas comment faire autrement...
Oui mais il faut mettre des parenthèses F(x) = 1/(x^2+5x)brets a écrit:f8 : u = x^2 + 5x donc F(x) = 1/x^2+5x ?
Re: Primitives
f1 : alors j'ai essayé de faire disparaitre le x^3 et le x^2, donc je divisais des deux côtés, pour qu'il reste seulement un x, pour prouver que x est plus grand que 2 donc que c'est bien une primitive.
f3 : parce que comme c'est l'exponentielle c'est toujours positif normalement donc je ne sais pas s'il faut prouver que c'est plus grand que 0
f4 : erreur de signe de ma part, c'est bien -5
f5 : je crois que c'est ce que j'ai fait comme c'est du type u'/u --> ln(u) ; u = ln(x) donc F(x)= ln(ln(x))
f6 : j'ai utilisé la même méthode que pour f1, sauf qu'au lieu de montrer que c'est > que 2 j'ai essayé de montrer que c'est > 0
f3 : parce que comme c'est l'exponentielle c'est toujours positif normalement donc je ne sais pas s'il faut prouver que c'est plus grand que 0
f4 : erreur de signe de ma part, c'est bien -5
f5 : je crois que c'est ce que j'ai fait comme c'est du type u'/u --> ln(u) ; u = ln(x) donc F(x)= ln(ln(x))
f6 : j'ai utilisé la même méthode que pour f1, sauf qu'au lieu de montrer que c'est > que 2 j'ai essayé de montrer que c'est > 0
Re: Primitives
f1
Une primitive est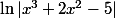
Pour écrire) il faut montrer que
il faut montrer que 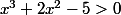 pour
pour 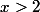 en étudiant la fonction x^3 + 2x^2 -5
en étudiant la fonction x^3 + 2x^2 -5
Par exemple, si au lieu de se placer sur [2,+oo[, on se plaçait sur [1,+oo[ alors ça ne marcherait pas puisque pour x=1, la fonction vaut -2 qui est négatif
f3
L'intervalle considéré est ]0,+oo[, la fonction est continue sur cet intervalle, il n'y a rien à faire de plus
f4
Peux-tu donner une primitive de la fonction g(x)=2x-5 ?
f5
Quel est le domaine de définition de f5 ?
f6
Il faut montrer que le fonction est positive sur IR en étudiant ses variations
Une primitive est
Pour écrire
Par exemple, si au lieu de se placer sur [2,+oo[, on se plaçait sur [1,+oo[ alors ça ne marcherait pas puisque pour x=1, la fonction vaut -2 qui est négatif
f3
L'intervalle considéré est ]0,+oo[, la fonction est continue sur cet intervalle, il n'y a rien à faire de plus
f4
Peux-tu donner une primitive de la fonction g(x)=2x-5 ?
f5
Quel est le domaine de définition de f5 ?
f6
Il faut montrer que le fonction est positive sur IR en étudiant ses variations
Re: Primitives
f1 : j'ai fait un tableau de variations et de signes de x^3 + 2x^2 -5 : la dérivée est 3x^2 + 4x donc delta est 16 donc il y a 2 racines. x1=0, x2= -1. Sur l'intervalle -1; 0 la fonction est positive. Sur 0 ; + l'infini c'est négatif et comme 2 appartient à cet intervalle alors x^3 + 2x^2 -5 >0 pour x> 2
f4 : oui. Une primitive de g(x) est x^2 -5x donc une primitive de f4 est 1/2e^x au carré - 5x ?
f5 : son domaine de définition est 1 ; + l'infini.
f6 : j'ai fait comme avec f1 et j'ai trouvé que la fonction est positive sur -1 ; 0 et négative sur 0 ; +l'infini mais on ne prend pas le 0 dans les intervalles. Pourtant il faut montrer l'inverse mais comme a >0 je ne vois pas où est mon erreur
f4 : oui. Une primitive de g(x) est x^2 -5x donc une primitive de f4 est 1/2e^x au carré - 5x ?
f5 : son domaine de définition est 1 ; + l'infini.
f6 : j'ai fait comme avec f1 et j'ai trouvé que la fonction est positive sur -1 ; 0 et négative sur 0 ; +l'infini mais on ne prend pas le 0 dans les intervalles. Pourtant il faut montrer l'inverse mais comme a >0 je ne vois pas où est mon erreur
Re: Primitives
Ouh la la !brets a écrit:f1 : j'ai fait un tableau de variations et de signes de x^3 + 2x^2 -5 : la dérivée est 3x^2 + 4x donc delta est 16 donc il y a 2 racines. x1=0, x2= -1. Sur l'intervalle -1; 0 la fonction est positive. Sur 0 ; + l'infini c'est négatif et comme 2 appartient à cet intervalle alors x^3 + 2x^2 -5 >0 pour x> 2
Revois ton calcul du discriminant. Soit dit en passant, ça ne sert à rien de le calculer ...
Ouibrets a écrit:f4 : oui. Une primitive de g(x) est x^2 -5x donc une primitive de f4 est 1/2e^x au carré - 5x ?
Non son domaine est ]0,1[ U ]1,+oo[brets a écrit:f5 : son domaine de définition est 1 ; + l'infini.
Peux-tu confirmer ton 1er message qui dit I=]0,+oo[ ?
La dérivée debrets a écrit:f6 : j'ai fait comme avec f1 et j'ai trouvé que la fonction est positive sur -1 ; 0 et négative sur 0 ; +l'infini mais on ne prend pas le 0 dans les intervalles. Pourtant il faut montrer l'inverse mais comme a >0 je ne vois pas où est mon erreur
Re: Primitives
f1 : pour calculer le discriminant on fait : b^2 - 4ac donc 4^2-4x3x0 = 16. Je ne vois pas où est mon erreur. Pourquoi ça ne sert à rien? Il y a une autre manière de trouver?
f5 : oui je confirme mon premier message. J'ai regardé sur ma calculatrice et son domaine de définition est bien 0 ; 1 U 1 ; + l'infini ( avec les crochets ). Donc je peux dire que F(x)= ln (ln(x)) est comprise dans I = 1 ; + l'infini ?
f6 : donc il faut que j'utilise 2x(2x^2-3) pour trouver le discriminant ou comme pour f1 ce n'est pas nécessaire?
f5 : oui je confirme mon premier message. J'ai regardé sur ma calculatrice et son domaine de définition est bien 0 ; 1 U 1 ; + l'infini ( avec les crochets ). Donc je peux dire que F(x)= ln (ln(x)) est comprise dans I = 1 ; + l'infini ?
f6 : donc il faut que j'utilise 2x(2x^2-3) pour trouver le discriminant ou comme pour f1 ce n'est pas nécessaire?
Re: Primitives
Oui j'ai raconté n'importe quoibrets a écrit:f1 : pour calculer le discriminant on fait : b^2 - 4ac donc 4^2-4x3x0 = 16. Je ne vois pas où est mon erreur. Pourquoi ça ne sert à rien? Il y a une autre manière de trouver?

Le discriminant vaut bien 0.
Ce qui ne va pas c'est ton calcul des 2 racines.
C'est inutile de calculer le discriminant car 3x^2 + 4x = x(3x+4) d'où on tire les racines facilement.
Pour trouver le domaine de définition de f5, pas besoin de calculatrice.brets a écrit:f5 : oui je confirme mon premier message. J'ai regardé sur ma calculatrice et son domaine de définition est bien 0 ; 1 U 1 ; + l'infini ( avec les crochets ). Donc je peux dire que F(x)= ln (ln(x)) est comprise dans I = 1 ; + l'infini ?
Il faut :
# x différent de 0
# ln(x) existe donc x > 0
#ln(x) différent de 0 donc x différent de 1.
Sur ]0,1[ et sur ]1,+oo[, une primitive de f5 est ln|ln|.
Sur ]1,+oo[ ln est positve donc une primitive de f5 est ln(ln).
Sur ]0,1[ ln est négative donc une primitive de f5 est ln(-ln).
Ce n'est pas nécessairebrets a écrit:f6 : donc il faut que j'utilise 2x(2x^2-3) pour trouver le discriminant ou comme pour f1 ce n'est pas nécessaire?
2x²-3=0 se résout facilement non ?
Re: Primitives
Merci pour ces explications.
f1 : pourquoi le discriminant vaut 0? J’ai trouvé 16
Pour la racine en utilisant 3x+4 j’ai trouvé -4/3 pour x donc il n’y a qu’une racine?
f5 : donc sur ]1;+ l’infini[ la primitive est ln(ln)?
f6 : oui donc en faisant 2x^2=3 puis x^2 = 3/2 je trouve x = racine carré de 3/2 et x = - racine carré de 3/2 mais -1,22 n’est pas sur |R donc je ne comprends pas
f1 : pourquoi le discriminant vaut 0? J’ai trouvé 16
Pour la racine en utilisant 3x+4 j’ai trouvé -4/3 pour x donc il n’y a qu’une racine?
f5 : donc sur ]1;+ l’infini[ la primitive est ln(ln)?
f6 : oui donc en faisant 2x^2=3 puis x^2 = 3/2 je trouve x = racine carré de 3/2 et x = - racine carré de 3/2 mais -1,22 n’est pas sur |R donc je ne comprends pas
Re: Primitives
f1
Oui le discriminant vaut 16
x(3x+4) =0 donne 2 racines : 0 et -4/3
f5
Oui
f6
-racine(3/2) est un réel non ?
Oui le discriminant vaut 16
x(3x+4) =0 donne 2 racines : 0 et -4/3
f5
Oui
f6
brets a écrit:mais -1,22 n’est pas sur |R donc je ne comprends pas
-racine(3/2) est un réel non ?
Re: Primitives
f6 : ah oui c’est vrai c’est un réel
J’ai construit le tableau de signes et variations et la fonction est négative sur l’intervalle -1,22 et 1,22 alors qu’on doit montrer qu’elle est positive sur |R .
Est ce que c’est grave si a un moment c’est négatif alors que le reste est positif?
J’ai construit le tableau de signes et variations et la fonction est négative sur l’intervalle -1,22 et 1,22 alors qu’on doit montrer qu’elle est positive sur |R .
Est ce que c’est grave si a un moment c’est négatif alors que le reste est positif?
Re: Primitives
Et pour f1 j’ai trouvé que la fonction est positive sur ]2 ; + l’infini [ donc je pense que c’est bon
Re: Primitives
brets a écrit:Et pour f1 j’ai trouvé que la fonction est positive sur ]2 ; + l’infini [ donc je pense que c’est bon
Oui
Re: Primitives
brets a écrit:f6 : ah oui c’est vrai c’est un réel
J’ai construit le tableau de signes et variations et la fonction est négative sur l’intervalle -1,22 et 1,22 alors qu’on doit montrer qu’elle est positive sur |R .
Est ce que c’est grave si a un moment c’est négatif alors que le reste est positif?
Ton tableau de signes n'est pas bon.
Tu as oublié 0 comme racine
Re: Primitives
Ah oui merci j’avais oublié le 0. Mais ce que je ne comprends pas c’est que il faut montrer que la fonction est positive sur |R alors que elle est négative sur certains intervalles
Re: Primitives
brets a écrit:Mais ce que je ne comprends pas c’est que il faut montrer que la fonction est positive sur |R alors que elle est négative sur certains intervalles
Sur quels intervalles ?
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 156 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
