Polynômes

[Mdiallo]

Salut les amis j'ai un problème avec une question avec les polynômes et j'aimerai que vous me proposez quelque chose pour m'aider, le voici :
Trouvez tous les polynômes P, à coefficient réels tels que :
P(a-b)+P(b-c)+P(c-a)=2P(a-b-c)
pour tous les triplets (a,b,c) de nombres réels tels que : ab+ bc+ ca =0.

[Ben314]

Salut,
Vu la dissymétrie de l'énoncé, c'est pas très intéressant comme question :
Si on prend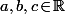 tels que 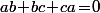alors on a , mais comme on a aussi 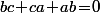c'est qu'on a aussi et ça signifie en particulier que .
Ensuite, si pour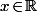 fixé, on cherche à résoudre le système 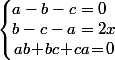, ça donne 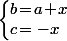puis 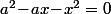qui admet clairement une racine réelle.
Donc et vu qu'avec 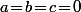on a c'est que le polynôme est nul.

Et là où on voit que ça a quasiment pas d'intérêt, c'est qu'on ne se sert absolument pas du fait que est un polynôme ni même de la dérivabilité ou de la continuité de la fonction P. Bref, à mon sens, ça sent plus que beaucoup que le bidule à été recopié à un moment ou un autre par quelqu'un qui y comprend pas grand chose et qui l'a recopié de travers . . .

[Sa Majesté]

https://www.maths-forum.com/lycee/polynomes-t200951.html