Bonjour, j'ai un dm de maths a rendre et je bloque sur une question.
Énoncé:
f(x)=(-x^2+3x-1)vx (attention, (vx)=racine carrée)
Q1.Dériver la fonction f sur }0;3} et montrer en détaillant les calculs, que l'on a f'(x)=-5x^2+9x-1/2vx.
Je vous prie de m'aider.Cordialement.
Maths fonction dérivée
8 messages
- Page 1 sur 1
Re: maths fonction dérivée
Bonsoir,
Je ne peux que te conseiller, avant de demander de l'aide, de repérer dans ton cours les formules donnant :
- la dérivée du produit de deux fonction :.{v(x)]')
- la dérivée de la fonction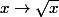
C'est une bien mauvaise méthode que de commencer par un exercice avant d'avoir étudié (lu ?) ton cours
Je ne peux que te conseiller, avant de demander de l'aide, de repérer dans ton cours les formules donnant :
- la dérivée du produit de deux fonction :
- la dérivée de la fonction
C'est une bien mauvaise méthode que de commencer par un exercice avant d'avoir étudié (lu ?) ton cours
Re: maths fonction dérivée
je connais bien mon cours, j'ai essayé de retourné le problème beaucoup de fois mais je n'arrive pas a résoudre ce problème,c'est pourquoi j,aimerai avoir de l'aide merci.
Re: maths fonction dérivée
de la forme
Tu as besoin des outils suivants :
- dérivée de la fonction
- dérivée de la fonction
- dérivée du produit de 2 fonctions
Et comme tu connais bien ton cours tu va pouvoir calculer cela immédiatement.
Re: maths fonction dérivée
le problème est de fait qu'en calculant je ne tombe pas sur f'(x), le fonction f est compliquée a dérivé c,est pour quoi j'aimerai qu'on me fournisse des éléments de réponsesles pour trouver f' merci bien.
Re: maths fonction dérivée
Comme tu ne donnes pas tes calculs, on ne peut pas t'aider pour voir où tu as fait une erreur.
Peux-tu donner ce que tu trouves pour :
- dérivée de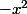
- dérivée de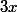
- dérivée de
- dérivée de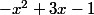
- dérivée de
- dérivée de.\sqrt{x}) en utilisant la dérivée d'un produit de 2 fonctions.
en utilisant la dérivée d'un produit de 2 fonctions.
Peux-tu donner ce que tu trouves pour :
- dérivée de
- dérivée de
- dérivée de
- dérivée de
- dérivée de
- dérivée de
Re: maths fonction dérivée
bonsoir,
une variante:
 est une puissance fractionnaire de x.
est une puissance fractionnaire de x.
on linéarise (on transforme un produit en somme):
=-x^{\frac{5}{2}}+3x^{\frac{3}{2}}-x^{\frac{1}{2}} \text{ car } \sqrt{x}=x^{\frac{1}{2}})
on dérive avec la formule'=\alpha \, x^{\alpha-1} \text{ avec } \alpha \text{ rationnel })
=-\frac{5}{2}x^{\frac{3}{2}}+\frac{9}{2}x^{\frac{1}{2}}-\frac{1}{2}x^{-\frac{1}{2}})
=(-\frac{5}{2}x+\frac{9}{2}-\frac{1}{2}x^{-1}) \sqrt{x})
on réduit au même dénominateur:
=\dfrac{-5x^2+9x-1}{2\sqrt{x}})
une variante:
on linéarise (on transforme un produit en somme):
on dérive avec la formule
on réduit au même dénominateur:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
