Merci à ceux qui prendront le temps de me répondre.
La question n°1 est " Résoudre dans R l'équation : x(4)-5/4(au carrée) + 3/8 = 0 "
Donc j'ai changer de repère je suis passée en T= x(carrée)
ce qui donne t(carrée) - 5/4 t + 3/8 = 0
j'ai trouver delta = 1/16
donc Delta > 0, il y a deux racines
x1 = (25/16 + racine de 1/16 )/2
et x2 = (25/16 - racine de 1/16)/2
donc St= {x1 ; x2)
mais on cherche les inconnues de x, donc on revient au changement d'inconnue : t=x(carrée)
donne deux posibilités : (25/16 + racine de 1/16 )/2=x(carrée)
ou (25/16 - racine de 1/16)/2=x(carrée)
donc après il faut que je trouve 0 = .... si ça donne deux facteurs genre (x+1)(x+3) puis je pourrai faire - si un produit est nul l'un de ces facteurs est nuls donc soit...etc
ou alors trouver directement x=...
->mais le problème c'est que je n'y arrive pas :/ et la question d'après me bloque encore plus
la voici "En déduire les solutions de l'équations : (cos x )(4) - 5/4 (cos x)(au carrée) + 3/8 = 0 "
je vois pas comment faire non plus après donc...
J'ai besoin vraiment besoin d'aide là.. merci.
Mathématique équation bicarrée
3 messages
- Page 1 sur 1
Bonsoir,
Tu es déjà bien parti! Au moins tu sais ce que tu fais et tu sais là ou tu bloques. C'est déjà une bonne chose.
En fait tu peux simplifier les expressions)
et)
Je te rappelle que 16=4^2 et que 1=1^2. donc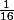
est un carré!
Ensuite, tu dois résoudre x^2 = x_1 et x^2 = x_2.
Comme x_1 et x_2 sont positifs, il y a à chaque fois deux solutions (une positive, une négative) qui sont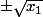 et
et 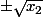 . Il n'y aura pas de racines empilées, en fait ça se simplifie pas mal.
. Il n'y aura pas de racines empilées, en fait ça se simplifie pas mal.
Une fois que tu as trouvé les quatre solutions de l'équation de départ, souffle un peu :zen:
Pour la suite, tu remarques que cos(x) joue le rôle que jouait x auparavant. Tu peux donc utiliser ce que tu as fait avant pour dire que cos(x) est dans l'ensemble des solutions de l'équation de la question 1.
Après, il ne reste plus qu'à résoudre cos(x) = quelque chose, mais il n'y a pas toujours de solutions, et quand il y en a ce n'est pas toujours des valeurs remarquables, il faut voir.
Bons calculs,
Luc
Piickles a écrit:Merci à ceux qui prendront le temps de me répondre.
La question n°1 est " Résoudre dans R l'équation : x(4)-5/4(au carrée) + 3/8 = 0 "
Donc j'ai changer de repère je suis passée en T= x(carrée)
ce qui donne t(carrée) - 5/4 t + 3/8 = 0
j'ai trouver delta = 1/16
donc Delta > 0, il y a deux racines
x1 = (25/16 + racine de 1/16 )/2
et x2 = (25/16 - racine de 1/16)/2
donc St= {x1 ; x2)
mais on cherche les inconnues de x, donc on revient au changement d'inconnue : t=x(carrée)
donne deux posibilités : (25/16 + racine de 1/16 )/2=x(carrée)
ou (25/16 - racine de 1/16)/2=x(carrée)
donc après il faut que je trouve 0 = .... si ça donne deux facteurs genre (x+1)(x+3) puis je pourrai faire - si un produit est nul l'un de ces facteurs est nuls donc soit...etc
ou alors trouver directement x=...
->mais le problème c'est que je n'y arrive pas :/ et la question d'après me bloque encore plus
la voici "En déduire les solutions de l'équations : (cos x )(4) - 5/4 (cos x)(au carrée) + 3/8 = 0 "
je vois pas comment faire non plus après donc...
J'ai besoin vraiment besoin d'aide là.. merci.
Tu es déjà bien parti! Au moins tu sais ce que tu fais et tu sais là ou tu bloques. C'est déjà une bonne chose.
En fait tu peux simplifier les expressions
et
Je te rappelle que 16=4^2 et que 1=1^2. donc
est un carré!
Ensuite, tu dois résoudre x^2 = x_1 et x^2 = x_2.
Comme x_1 et x_2 sont positifs, il y a à chaque fois deux solutions (une positive, une négative) qui sont
Une fois que tu as trouvé les quatre solutions de l'équation de départ, souffle un peu :zen:
Pour la suite, tu remarques que cos(x) joue le rôle que jouait x auparavant. Tu peux donc utiliser ce que tu as fait avant pour dire que cos(x) est dans l'ensemble des solutions de l'équation de la question 1.
Après, il ne reste plus qu'à résoudre cos(x) = quelque chose, mais il n'y a pas toujours de solutions, et quand il y en a ce n'est pas toujours des valeurs remarquables, il faut voir.
Bons calculs,
Luc
Luc a écrit:Bonsoir,
Tu es déjà bien parti! Au moins tu sais ce que tu fais et tu sais là ou tu bloques. C'est déjà une bonne chose.
En fait tu peux simplifier les expressions)
et)
Je te rappelle que 16=4^2 et que 1=1^2. donc
est un carré!
Ensuite, tu dois résoudre x^2 = x_1 et x^2 = x_2.
Comme x_1 et x_2 sont positifs, il y a à chaque fois deux solutions (une positive, une négative) qui sontet
. Il n'y aura pas de racines empilées, en fait ça se simplifie pas mal.
Une fois que tu as trouvé les quatre solutions de l'équation de départ, souffle un peu :zen:
Pour la suite, tu remarques que cos(x) joue le rôle que jouait x auparavant. Tu peux donc utiliser ce que tu as fait avant pour dire que cos(x) est dans l'ensemble des solutions de l'équation de la question 1.
Après, il ne reste plus qu'à résoudre cos(x) = quelque chose, mais il n'y a pas toujours de solutions, et quand il y en a ce n'est pas toujours des valeurs remarquables, il faut voir.
Bons calculs,
Luc
Merci beaucoup
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
