La logique

[maths-girl]

Bonjour,
j'aimerais bien que quelqu'un m'explique coment résoudre cet exo:

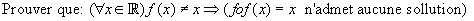
Merci

[emdro]

Bonjour,

si tu définis
f(x)=-x lorsque x est non nul et f(0)=1,

* on est d'accord que f(x) n'est jamais égal à x.
* Pourtant, pour x différent de 0, f(f(x))=f(-x)=-(-x)=x. Donc l'équation fof(x)=x admet une infinité de solutions.

Ce que tu demandes de démontrer est faux!

[emdro]

Bien-sûr, mon contre-exemple est une fonction non continue.
C'est vrai pour une fonction continue.

[maths-girl]

Pardon, j'ai oublié de signalé que f est une fonction continue sur l'ensemble IR

[emdro]

Cela change tout!

Dans ce cas, tu n'auras aucune difficulté à démontrer qu'on a soit toujours f(x)x. Raisonne par l'absurde: si f(a)b, par le théorème des valeurs intermédaires appliqué à la fonction f(x)-x, on aurait un réel c tel que f(c)=c.

Si f(x). :zen:

[maths-girl]

Raisonne par l'absurde: si f(a)b, par le théorème des valeurs intermédaires appliqué à la fonction f(x)-x, on aurait un réel c tel que f(c)=c.

Si f(x). :zen:

J'ai pas compris cette partie.. :marteau:
J'ai fait :
f(x)>x -> f(f(x))>f(x) -> fof>x
f(x) f(f(x)) fof<x
donc fof est differente de x
Mais le prof m'a dit que c'est fait!!

[maths-girl]

il m'a dit qu'il faut supposer de réel a et b , mais je ne sais pas pourquoi et comment faire la suite...

[emdro]

Que c'est fait ou que c'est faux?

[maths-girl]

pardon "faux" :briques:

[emdro]

Il y a un truc faux: fof
Ensuite, il y a le fait que tu n'as pas démontré que:
* soit f(x)* soit f(x)>x pour tout x réel.

Tu pourrais très bien avoir une fonction qui donne parfois f(x)>x et parfois f(x)
Pour démontrer cela, il faut utiliser la fonction auxiliaire g(x)=f(x)-x, et raisonner par l'absurde (avec a et b comme moi).

[maths-girl]

Merci infiniment !!