[ENTRAINEMENT 1ere S] Fonctions polynômes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 11 Sep 2009, 12:55
par Anonyme » 11 Sep 2009, 12:55
Pour
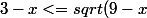)
C'est la plus interessante parmis toutes les equations qui la precede
J'ai trouve
x appartient a [0,9] J'aime pas trop ma demonstration alors j'aimerais voir la correction (si bien entendu mon resultat est correcte)
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 15:51
par Euler911 » 11 Sep 2009, 15:51
la loi du reste dit que le reste de la division d'un polynôme P(x) par (x-a) vaut
P(a)... ça implique entre autre l'existence d'un polynôme Q(x) tel que:
=(x-a)Q(x)+P(a)\\<br />Deg(P)> Deg(Q)<br />\end{array}\right.)
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 15:53
par Euler911 » 11 Sep 2009, 15:53
Sinon, pour l'inéquation... suffit de faire un tableau de signe:| et de trouver le domaine de la fonction f(x)=3-x-V(9-x).
-
mito94
- Membre Relatif
- Messages: 165
- Enregistré le: 21 Juin 2009, 08:03
-
 par mito94 » 11 Sep 2009, 15:55
par mito94 » 11 Sep 2009, 15:55
si çà peut aider , dites vous que généralement les racines dites evidentes sont compris en [-2;2]
-
Anonyme
 par Anonyme » 11 Sep 2009, 15:55
par Anonyme » 11 Sep 2009, 15:55
Euler911 a écrit:Sinon, pour l'inéquation... suffit de faire un tableau de signe:| et de trouver le domaine de la fonction f(x)=3-x-V(9-x).
Pas compris pourrais tu le faire ?
merci
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 15:56
par Euler911 » 11 Sep 2009, 15:56
mito94 a écrit:si çà peut aider , dites vous que généralement les racines dites evidentes sont compris en [-2;2]
?! moi pas comprendre...:s
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 16:01
par Euler911 » 11 Sep 2009, 16:01
Qmath a écrit:Pas compris pourrais tu le faire ?
merci
Tu as vu que 3-x=V(9-x) qd x =0. Reste à trouver les signes de f(x)=3-x-V(9-x) de part et d'autre de 0, c'est pas bien compliqué... cherche f(-1), f(1) et puisque f est continue, c'est suffisant.
-
Anonyme
 par Anonyme » 11 Sep 2009, 16:06
par Anonyme » 11 Sep 2009, 16:06
Avec cette methode je retrouve ma reponse.
mais que veut dire f est continu ?
fonction continue veut dire quoi ?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 16:12
par Euler911 » 11 Sep 2009, 16:12
Qmath a écrit:Avec cette methode je retrouve ma reponse.
Tu trouves quoi finalement?
mais que veut dire f est continu ?
fonction continue veut dire quoi ?
Ne fait pas attention à ça; j'ai oublié que l'exercice était adressé à des personnes en 2nd... tu verras ce que ça veut dire plus tard (l'année prochaine normalement).
-
Anonyme
 par Anonyme » 11 Sep 2009, 16:30
par Anonyme » 11 Sep 2009, 16:30
Euler911 a écrit:Tu trouves quoi finalement?
x appartient [0,9]
mais mon raisonnement est plus complique avec beaucoup d'intervalles...
Euler911 a écrit:Ne fait pas attention à ça; j'ai oublié que l'exercice était adressé à des personnes en 2nd... tu verras ce que ça veut dire plus tard (l'année prochaine normalement).
Je rentre en 1ere S dans quelques jour donc je pense que je comprendrais ton explication.
Tu viens de me rappeler de mettre mon profil a jour :zen:
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 18:24
par Euler911 » 11 Sep 2009, 18:24
C'est bien ce qu'il faut trouver pour l'inéquation:-)
Je préfère ne pas t'expliquer ce que signifie "fonction continue"... ça prendrait beaucoup de temps; et ton prof de maths le fera bien mieux que moi:-) Pour comprendre ce qu'est la continuité, il faut comprendre d'abords ce qu'est une limite par exemple, et le chapitre sur les limites est un gros chapitre de 1re...
Néanmoins, rien ne t'interdit de lire des cours sur internet (je pense entre autre au cours sur les limites et sur la continuité que propose le site Bacamath) ou de lire ce qu'il faut dans ton manuel (si tu en as un;-) .
-
Anonyme
 par Anonyme » 11 Sep 2009, 18:37
par Anonyme » 11 Sep 2009, 18:37
Je verrais un peu de quoi ca parle
2) Trouver une fonction périodique de période 2006.
C'est la premiere fois que j'entend parler de fonction periodique differentes des fonctions trigonometrique alors je voulais demander si ma reponse est correcte
reponse(en blanc):
f(x)=x % 2006 le reste de la division par 2006Si c'est pas cela, ca sera tres interessant de chercher
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 19:05
par Euler911 » 11 Sep 2009, 19:05
La fonction que tu donnes est bien périodique!
Mais attention, ta fonction est définie de
N vers
N 
La congruence n'étant valable qu'entre des entiers:) Tu peux cependant trouver un prolongement de ta fonction dans l'ensemble des réels. Mais c'est à toi de la trouver:-)
-
Anonyme
 par Anonyme » 11 Sep 2009, 19:16
par Anonyme » 11 Sep 2009, 19:16
Euler911 a écrit:La fonction que tu donnes est bien périodique!
Mais attention, ta fonction est définie de
N vers
N 
La congruence n'étant valable qu'entre des entiers:) Tu peux cependant trouver un prolongement de ta fonction dans l'ensemble des réels. Mais c'est à toi de la trouver:-)
J'ai pense a ca
et j'avais trouve:
f(x)= le reste de la division de l'entier le plus proche de x par 2006
mais je sais pas comment ecrire l'entier le plus proche mathématiquement dans une fonctionc'est correcte ?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 19:24
par Euler911 » 11 Sep 2009, 19:24
Je ne sais pas ce que tu entends par entier le plus proche, mais il existe une fonction qui s'appelle partie entière, elle est notée
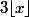
, par exemple:
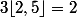
,
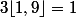
,
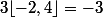
etc.
-
Anonyme
 par Anonyme » 11 Sep 2009, 19:33
par Anonyme » 11 Sep 2009, 19:33
Euler911 a écrit:Je ne sais pas ce que tu entends par entier le plus proche, mais il existe une fonction qui s'appelle partie entière, elle est notée
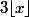
, par exemple:
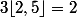
,
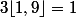
,
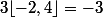
etc.
maintenant que je connais l'existance d'une fonction qui donne la partie entiere j'ai plus besoin de ce qui precede
la fonction en question sera :
f(x)= [x]%2006juste une chose pourquoi
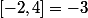
et pas
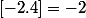
?
Merci pour tout Euler :zen:
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 11 Sep 2009, 19:40
par Euler911 » 11 Sep 2009, 19:40
Qmath a écrit:juste une chose pourquoi
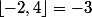
et pas
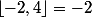
?
Merci pour tout Euler :zen:
La définition de la partie entière que j'utilise est la suivante:
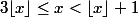 EDIT: ok pour ta fonction:)
EDIT: ok pour ta fonction:)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Sep 2009, 09:59
par Timothé Lefebvre » 12 Sep 2009, 09:59
Salut :happy3:
Alors, voyons l'exercice 1. Ok pour les racines évidentes. Seconde question, pour prouver l'existence de Q. Le polynôme P admet deux racines distinctes -1 et 1. On peut dire qu'il existe un polynôme

tel que :

soit

.
Or,

est un polynôme du quatrième degré, on en déduit donc que

est de degré 2.
Pour la question 3 on fera une factrisation puis un tableau de signes.
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 12 Sep 2009, 10:03
par Euler911 » 12 Sep 2009, 10:03
Timothé Lefebvre a écrit:. On peut dire qu'il existe un polynôme

On peut dire... mais ça ne justifie pas:-)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Sep 2009, 10:11
par Timothé Lefebvre » 12 Sep 2009, 10:11
Ah si, en fait il existe un polynôme Q tel que je l'ai donné !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
La congruence n'étant valable qu'entre des entiers:) Tu peux cependant trouver un prolongement de ta fonction dans l'ensemble des réels. Mais c'est à toi de la trouver:-)
, par exemple:
,
,
etc.
 tel que :
tel que : soit
soit  .
. est un polynôme du quatrième degré, on en déduit donc que
est un polynôme du quatrième degré, on en déduit donc que  est de degré 2.
est de degré 2.