Bonjour Voici un exercice de mon dm de maths
On considère la suite Un tel que U0 = 2 et Un + 1 =( 2 Un + 4) / (Un - 1 )
1.Calculer la valeur exacte de U1 U2 U3
2.soit Vn =( Un - 4 )/ (Un +1) démontrer que la suite vn est géométrique et préciser sa raison
3. En déduire vn explicitement en fonction de n( on calculera notamment V0 )
4. En déduire Un explicitement en fonction de n
5. Vérifier que la formule explicite de la question 4 confirme les résultats de la question 1
6. À l'aide de la question 4 calculer limite de Un
Merci d'avance pour votre aide
Étude d'une suite homographique
10 messages
- Page 1 sur 1
Re: Étude d'une suite homographique
Salut !
Oui et alors qu'as-tu fait ? Où bloques-tu ?
Oui et alors qu'as-tu fait ? Où bloques-tu ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Étude d'une suite homographique
1. J'ai trouvé U1 = 8 ,U2 = 20 / 7 et U3 = 68 / 13
2. Vn+1=(Un+1 - 4) / (Un+1 +1) à la fin je trouve( - 2 / 3 )Vn
Donc vn est une suite géométrique de raison - 2 / 3
3. On calcule V0=(U0-4)/(U0+1)=-2/3
Alors vn = V0 x puissance n = (-2/3)x(-2/3) puissance n
Est ce que jusque là c'est bon ?
2. Vn+1=(Un+1 - 4) / (Un+1 +1) à la fin je trouve( - 2 / 3 )Vn
Donc vn est une suite géométrique de raison - 2 / 3
3. On calcule V0=(U0-4)/(U0+1)=-2/3
Alors vn = V0 x puissance n = (-2/3)x(-2/3) puissance n
Est ce que jusque là c'est bon ?
Re: Étude d'une suite homographique
Oui, parfait seulement à la question 3, tu peux écrire carrément que, pour tout 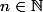 ,
, 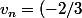^{n+1}) .
.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Étude d'une suite homographique
Pour la question 4, utilise les deux dernières questions. La question 2 te donne une égalité liant  et
et  et tu connais
et tu connais  en fonction de
en fonction de  d'après la question 3. Il te suffit donc d'exprimer
d'après la question 3. Il te suffit donc d'exprimer  en fonction de
en fonction de  .
.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Étude d'une suite homographique
Pour la 4 j'ai utilisé Vn= (Un-4)/(Un+1)
Et je trouve a fin -2Vn-3
Sauf que ça ne vérifie pas mes premier résultats
Et je trouve a fin -2Vn-3
Sauf que ça ne vérifie pas mes premier résultats
Re: Étude d'une suite homographique
Je ne comprends pas comment tu obtiens un tel résultat... Ca veut dire quoi j'obtiens à fin 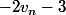 ? Tu veux dire
? Tu veux dire 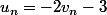 ?
?
Montre que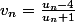 équivaut à
équivaut à 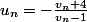 .
.
Montre que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Étude d'une suite homographique
Non, ça n'a pas de sens ce que tu écris. Je t'ai dit que dans la question 2, on te donne  en fonction de
en fonction de  . Or on connait
. Or on connait  et on veut
et on veut  donc il faut exprimer
donc il faut exprimer  en fonction de
en fonction de  .
.
Si je dit que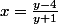 (ici
(ici  est exprimé en fonction de
est exprimé en fonction de  ), comment exprimer
), comment exprimer  en fonction de
en fonction de  ?
?
Si je dit que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
